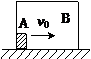题目内容
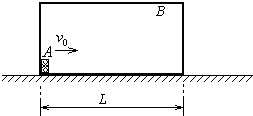 如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为
如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为| M | 5 |
(1)A与B第一次碰撞前,B是否运动?
(2)若A第一次与B碰后瞬间向左运动的速率为v1,求此时矩形盒B的速度大小;
(3)当B停止运动时,A的速度是多少?
分析:(1)A与B第一次碰撞前,由题意有B受到的最大静摩擦力为μ(M+
)g=
,而A给B的摩擦力为μ
g<
所以B不运动
(2)AB碰撞过程动量守恒,根据动量守恒定律列式求解即可.
(3)当B停止运动时,A继续向右滑行s(s<L)后停止,根据动能定理列式求解即可.
| M |
| 5 |
| 6μMg |
| 5 |
| M |
| 5 |
| 6μMg |
| 5 |
(2)AB碰撞过程动量守恒,根据动量守恒定律列式求解即可.
(3)当B停止运动时,A继续向右滑行s(s<L)后停止,根据动能定理列式求解即可.
解答:解:(1)A与B第一次碰撞前,A对B的摩擦力为
f1=μN1=
地面对B的最大静摩擦力为
f2=μN2=μ(M+
)g=
f1<f2 故A与B第一次碰撞前,B不运动
(2)设A第一次碰前速度为v,碰后B的速度为v2,A的速度为v1
对A由动能定理得:
-μ
gL=
v2-
v02
碰撞过程中动量守恒有
v=
v1+Mv2
解得 v2=
(
+v1)
(3)当B停止运动时,A继续向右滑行s(s<L)后停止,设B停止时,A的速度为vA,则由动能定理得
-μ
gs=-
vA2
解得 vA=
答; (1)A与B第一次碰撞前,B不运动;
(2)若A第一次与B碰后瞬间向左运动的速率为v1,求此时矩形盒B的速度大小v2=
(
+v1);
(3)当B停止运动时,A的速度是vA=
.
f1=μN1=
| μMg |
| 5 |
地面对B的最大静摩擦力为
f2=μN2=μ(M+
| M |
| 5 |
| 6μMg |
| 5 |
f1<f2 故A与B第一次碰撞前,B不运动
(2)设A第一次碰前速度为v,碰后B的速度为v2,A的速度为v1
对A由动能定理得:
-μ
| M |
| 5 |
| 1 |
| 2 |
| M |
| 5 |
| 1 |
| 2 |
| M |
| 5 |
碰撞过程中动量守恒有
| M |
| 5 |
| M |
| 5 |
解得 v2=
| 1 |
| 5 |
| v02-2μgL |
(3)当B停止运动时,A继续向右滑行s(s<L)后停止,设B停止时,A的速度为vA,则由动能定理得
-μ
| M |
| 5 |
| 1 |
| 2 |
| M |
| 5 |
解得 vA=
| 2μgs |
答; (1)A与B第一次碰撞前,B不运动;
(2)若A第一次与B碰后瞬间向左运动的速率为v1,求此时矩形盒B的速度大小v2=
| 1 |
| 5 |
| v02-2μgL |
(3)当B停止运动时,A的速度是vA=
| 2μgs |
点评:本题考查动能定理和动量守恒定律的综合应用,应熟练掌握其公式.

练习册系列答案
相关题目
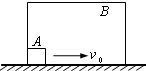 如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为
如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为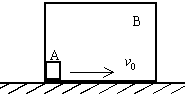 如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为M/5可视为质点的物体A,A与B、B与地面间的动摩擦因数分别为μ1、μ2,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右且与矩形盒B左、右侧壁垂直的水平速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B最后一次碰撞后,B停止运动,A则继续向右滑行距离S(S<L)后也停止运动,则:
如图所示,矩形盒B的质量为M,底部长度为L,放在水平面上,盒内有一质量为M/5可视为质点的物体A,A与B、B与地面间的动摩擦因数分别为μ1、μ2,开始时二者均静止,A在B的左端.现瞬间使物体A获得一向右且与矩形盒B左、右侧壁垂直的水平速度v0,以后物体A与盒B的左右壁碰撞时,B始终向右运动.当A与B最后一次碰撞后,B停止运动,A则继续向右滑行距离S(S<L)后也停止运动,则: