题目内容
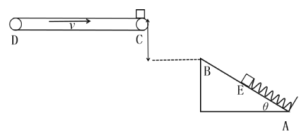
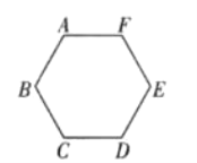
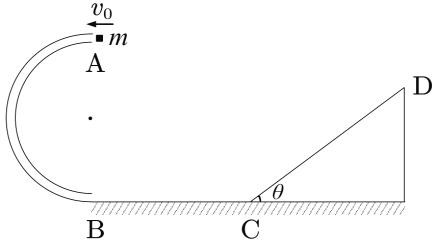
【题目】如图所示,AB为一固定在水平面上的半圆形细圆管轨道,轨道内壁粗糙,其半径为R且远大于细管的内径,轨道底端与水平轨道BC相切于B点。水平轨道BC长为2R,动摩擦因数为μ1=0.5,右侧为一固定在水平面上的粗糙斜面。斜面CD足够长,倾角为θ=37°,动摩擦因数为μ2=0.8。一质量为m,可视为质点的物块从圆管轨道顶端A点以初速度![]() 水平射入圆管轨道,运动到B点时对轨道的压力为自身重力的5倍,物块经过C点时速度大小不发生变化。sin37°=0.6,cos37°=0.8,重力加速度为g,求:
水平射入圆管轨道,运动到B点时对轨道的压力为自身重力的5倍,物块经过C点时速度大小不发生变化。sin37°=0.6,cos37°=0.8,重力加速度为g,求:
(1)物块从A点运动到B点的过程中,阻力所做的功;
(2)物块最终停留的位置。
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)物块到B点时,设轨道对其支持力为N,由牛顿第三定律知
![]()
由牛顿第二定律
![]()
解得
![]()
A到B的过程,由动能定理
![]()
得
![]()
(2)设物块沿斜面上升的最大位移为![]() ,由动能定理
,由动能定理
![]()
其中
![]() ,
,![]()
得
![]()
因![]() ,故物块在速度减为零之后不会下滑,物体最终会静止在斜面上距离
,故物块在速度减为零之后不会下滑,物体最终会静止在斜面上距离![]() 点
点![]() 的位置。
的位置。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目