题目内容
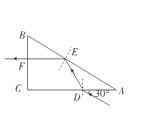
【题目】图示为直角三棱镜的截面ABC其中∠B=60°,直角边AC的长度为L,一束单色光从D点以与AC边成30°角入射到棱镜中,已知CD=2AD,棱镜对该单色光的折射率为![]() ,光在真空中的速度为c。求:
,光在真空中的速度为c。求:

①光线从BC边射出时与该边的夹角;
②此单色光通过三棱镜的时间。
【答案】(1)光线从BC边射出时与该边的夹角为900;(2)![]()
【解析】
(1)由折射定律和几何关系可以确定光射到AB边上时发生全反射,从而可以知道单色光从BC边垂直射出。
(2)由几何关系得光在三棱镜中通过的距离,由v=![]() 得单色光在三棱镜中的速度,即可求时间。
得单色光在三棱镜中的速度,即可求时间。
(1)由题意可知,单色光射到AC边的入射角i=600,设光从AC边入射的折射角为r,由折射定律可知:n=![]() ,可得:r=300,由几何关系可知,该单色光在AB边的入射角也是600,设单色光从三棱镜向空气发生全反射的临界角为C,由于
,可得:r=300,由几何关系可知,该单色光在AB边的入射角也是600,设单色光从三棱镜向空气发生全反射的临界角为C,由于![]() =
=![]() =
=![]() =
=![]() ,故光射到AB边上时发生全反射,光路如下图所示,反射光线与AB边的夹角是300,所以单色光从BC边垂直射出,即光线从BC边射出时与该边的夹角为900。
,故光射到AB边上时发生全反射,光路如下图所示,反射光线与AB边的夹角是300,所以单色光从BC边垂直射出,即光线从BC边射出时与该边的夹角为900。
(2)由几何关系可知,光在三棱镜中通过的距离为:
X=DE+FE=![]() +(
+(![]() -
-![]() )=
)=![]()
单色光在三棱镜中的速度:v=![]() =
=![]()
此单色光通过三棱镜的时间:t=![]() =
=![]()

练习册系列答案
相关题目