题目内容
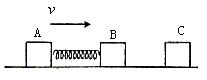
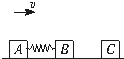 用轻弹簧相连的质量均为2kg的A.B两物块都以v=6m/s的速度在光滑的水平地面上运动,弹簧处于原长.质量4kg的物块C静止在前方,如图所示.B与C碰撞后粘在一起运动.在以后的运动过程中
用轻弹簧相连的质量均为2kg的A.B两物块都以v=6m/s的速度在光滑的水平地面上运动,弹簧处于原长.质量4kg的物块C静止在前方,如图所示.B与C碰撞后粘在一起运动.在以后的运动过程中(1)当弹簧的弹性势能最大时,物体A的速度多大;
(2)弹性势能的最大值是多大;
(3)A的速度有可能向左吗?判断并通过计算说明理由.
分析:(1)B与C发生碰撞后,B的速度减小,BC一起向右运动.A物体没有参加碰撞,速度不变,继续向右运动,这样弹簧被压缩,当三者速度相同时,弹簧压缩量最大,弹性势能最大,根据动量守恒求出物体A的速度.
(2)根据动量守恒求出BC碰撞后的共同速度.由机械能守恒求解弹性势能的最大值.
(3)假设A速度向左,根据动量守恒研究BC共同体的速度,分析系统的总机械能的变化情况,若总机械能增加,则不可能.
(2)根据动量守恒求出BC碰撞后的共同速度.由机械能守恒求解弹性势能的最大值.
(3)假设A速度向左,根据动量守恒研究BC共同体的速度,分析系统的总机械能的变化情况,若总机械能增加,则不可能.
解答:解:
(1)当A、B、C三者的速度相等时弹簧的弹性势能最大.
由A、B、C三者组成的系统动量守恒得:
(mA+mB)v=(mA+mB+mC)VA
解得:VA=3m/s
(2)B、C碰撞时,B、C系统动量守恒,设碰后瞬间两者的速度为v1,则:
mBv=(mB+mC)v1
解得:v1=2m/s
设弹簧的弹性势能最大为EP,根据机械能守恒得:
EP=
(mB+mC)
+
mAv2-
(mA+mB+mC)
代入解得为:EP=12J.
(3)A不可能向左运动.
系统动量守恒,(mA+mB)v=mAvA+(mB+mC)vB
假设A向左,vA<0,vB>4m/s,此时A、B、C动能之和为
E′=
mA
+
(mB+mC)
>
(mB+mC)
=48J
实际上系统的机械能:E=
(mB+mC)
+
mAv2=48J
根据能量守恒定律,E′>E,违反了能量守恒定律,是不可能的.
答:
(1)当弹簧的弹性势能最大时,物体A的速度为3m/s;
(2)弹性势能的最大值是12J;
(3)A的速度不可能向左,若A向左,违反了能量守恒定律.
(1)当A、B、C三者的速度相等时弹簧的弹性势能最大.
由A、B、C三者组成的系统动量守恒得:
(mA+mB)v=(mA+mB+mC)VA
解得:VA=3m/s
(2)B、C碰撞时,B、C系统动量守恒,设碰后瞬间两者的速度为v1,则:
mBv=(mB+mC)v1
解得:v1=2m/s
设弹簧的弹性势能最大为EP,根据机械能守恒得:
EP=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| V | 2 A |
代入解得为:EP=12J.
(3)A不可能向左运动.
系统动量守恒,(mA+mB)v=mAvA+(mB+mC)vB
假设A向左,vA<0,vB>4m/s,此时A、B、C动能之和为
E′=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 B |
实际上系统的机械能:E=
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
根据能量守恒定律,E′>E,违反了能量守恒定律,是不可能的.
答:
(1)当弹簧的弹性势能最大时,物体A的速度为3m/s;
(2)弹性势能的最大值是12J;
(3)A的速度不可能向左,若A向左,违反了能量守恒定律.
点评:本题是含有非弹性碰撞的过程,不能全过程列出机械能守恒方程:EP=
mAv2+
mBv2-
(mA+mB+mC)
这是学生经常犯的错误.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| V | 2 A |
这是学生经常犯的错误.

练习册系列答案
相关题目
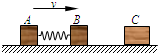 (2007?南京一模)如右图所示,用轻弹簧相连的质量均为2kg的A、B两物块都以v=6m/s的速度在光滑水平地面上运动,弹簧处于原长,质量4kg的物块C静止在前方,B与C碰撞后二者粘在一起运动.在以后的运动中,求:
(2007?南京一模)如右图所示,用轻弹簧相连的质量均为2kg的A、B两物块都以v=6m/s的速度在光滑水平地面上运动,弹簧处于原长,质量4kg的物块C静止在前方,B与C碰撞后二者粘在一起运动.在以后的运动中,求: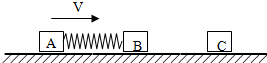 用轻弹簧相连的质量均为2kg的A、B两物块都以v=6m/s的速度在光滑的水平面上运动,弹簧处于原长,质量为4kg的物块C在前方静止.把B和C碰后共同运动.如图所示.求:
用轻弹簧相连的质量均为2kg的A、B两物块都以v=6m/s的速度在光滑的水平面上运动,弹簧处于原长,质量为4kg的物块C在前方静止.把B和C碰后共同运动.如图所示.求: