题目内容
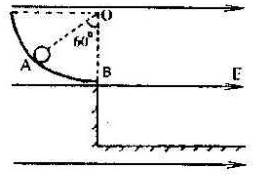 在水平方向的匀强电场中,位于竖直平面内的1/4光滑圆弧轨道,轨道半径为R,B端与竖直墙相接,OB沿竖直方向.已知B点距地面高度为h,电场强度大小为E,方向水平向右.一个质量为m,电量为q的带正电的小球从图中圆弧的A点无初速释放后,沿圆弧轨道运动.
在水平方向的匀强电场中,位于竖直平面内的1/4光滑圆弧轨道,轨道半径为R,B端与竖直墙相接,OB沿竖直方向.已知B点距地面高度为h,电场强度大小为E,方向水平向右.一个质量为m,电量为q的带正电的小球从图中圆弧的A点无初速释放后,沿圆弧轨道运动.(1)求小球刚要运动到B点时的速度及小球对轨道压力的大小;
(2)若小球到达B点时电场突然消失,求小球落地点距B点的水平距离.
分析:(1)从释放至B点,根据动能定理求出B点速度,根据牛顿第二定律求出压力的大小
(2)根据平抛运动规律求出小球落地点距B点的水平距离.
(2)根据平抛运动规律求出小球落地点距B点的水平距离.
解答:解:(1)设球到B点时的速度为vB,从释放至B点,根据动能定理:
mgR(1-cosθ)+qERsinθ=
m
vB=
=
根据牛顿第二定律得:
N-mg=
解得:N=3mg-2mgcosθ+2qEsinθ=2mg+
qE
根据牛顿第三定律得:小球对轨道压力的大小N′=N=3mg-2mgcosθ+2qEsinθ
(2)若小球到达B点时电场突然消失,小球离开B点后做平抛运动,
根据平抛运动规律得:
x=vBt
h=
gt2
x=
=
答:(1)到B点时的速度是
,小球对轨道压力的大小是2mg+
qE.
(2)小球落地点距B点的水平距离是
.
mgR(1-cosθ)+qERsinθ=
| 1 |
| 2 |
| v | 2 B |
vB=
|
gR+
|
根据牛顿第二定律得:
N-mg=
| ||
| R |
解得:N=3mg-2mgcosθ+2qEsinθ=2mg+
| 3 |
根据牛顿第三定律得:小球对轨道压力的大小N′=N=3mg-2mgcosθ+2qEsinθ
(2)若小球到达B点时电场突然消失,小球离开B点后做平抛运动,
根据平抛运动规律得:
x=vBt
h=
| 1 |
| 2 |
x=
|
2hR+
|
答:(1)到B点时的速度是
gR+
|
| 3 |
(2)小球落地点距B点的水平距离是
2hR+
|
点评:本题整合了动能定理、牛顿第二定律的应用,关键是清楚物体的运动过程.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 如图所示,ABCDF为一绝缘光滑轨道,竖直放置在水平方向的 匀强电场中,BCDF是半径为R的圆形轨道,已知电场强度为E,今有质量为m的带电小球在电场力作用下由静止从A点开始沿轨道运动,小球受到的电场力和重力大小相等,要使小球沿轨道做圆周运动,则AB间的距离至少为多大?
如图所示,ABCDF为一绝缘光滑轨道,竖直放置在水平方向的 匀强电场中,BCDF是半径为R的圆形轨道,已知电场强度为E,今有质量为m的带电小球在电场力作用下由静止从A点开始沿轨道运动,小球受到的电场力和重力大小相等,要使小球沿轨道做圆周运动,则AB间的距离至少为多大? 如图所示,A、B两个带电小球可以看成点电荷,用两等长绝缘细线悬挂起来,在水平方向的匀强电场中,A、B静止,且悬线都保持竖直,已知A、B相距3cm,A的带电量为qA=+2.0×10-9 C.已知静电力常量k=9.0×109N?m2/C2.求:
如图所示,A、B两个带电小球可以看成点电荷,用两等长绝缘细线悬挂起来,在水平方向的匀强电场中,A、B静止,且悬线都保持竖直,已知A、B相距3cm,A的带电量为qA=+2.0×10-9 C.已知静电力常量k=9.0×109N?m2/C2.求: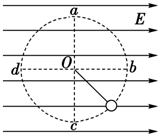 如图所示,在水平方向的匀强电场中,绝缘细线的一端固定在O点,另一端系一带正电的质量为m的小球在竖直平面内做圆周运动(轨道半径为r),小球所受的电场力大小等于
如图所示,在水平方向的匀强电场中,绝缘细线的一端固定在O点,另一端系一带正电的质量为m的小球在竖直平面内做圆周运动(轨道半径为r),小球所受的电场力大小等于