题目内容
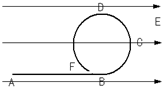
 如图所示,ABCDF为一绝缘光滑轨道,竖直放置在水平方向的 匀强电场中,BCDF是半径为R的圆形轨道,已知电场强度为E,今有质量为m的带电小球在电场力作用下由静止从A点开始沿轨道运动,小球受到的电场力和重力大小相等,要使小球沿轨道做圆周运动,则AB间的距离至少为多大?
如图所示,ABCDF为一绝缘光滑轨道,竖直放置在水平方向的 匀强电场中,BCDF是半径为R的圆形轨道,已知电场强度为E,今有质量为m的带电小球在电场力作用下由静止从A点开始沿轨道运动,小球受到的电场力和重力大小相等,要使小球沿轨道做圆周运动,则AB间的距离至少为多大?分析:要使小球在圆轨道上做圆周运动,小球在“最高”点不脱离圆环.这“最高”点并不是D点,可采用等效重力场的方法进行求解.
对小球受力分析可知,小球在混合场中的最高点,此时小球的速度应该为零,在由动能定理可以求得AB间的距离.
对小球受力分析可知,小球在混合场中的最高点,此时小球的速度应该为零,在由动能定理可以求得AB间的距离.
解答:解:重力场和电场合成等效重力场,其方向为电场力和重力的合力方向,与竖直方向的夹角(如图所示)
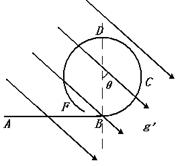
tanθ=
=1
θ=45°
等效重力加速度g′=
=
g
在等效重力场的“最高”点,小球刚好不掉下来时,由牛顿第二定律可得,
mg′=
v=
从A到等效重力场的“最高”点,由动能定理
qE(L-Rsin45°)-mg(R+Rcos45°)=
mv2-0
L=
=(1+
)R
答:AB间的距离至少为(1+
)R.

tanθ=
| mg |
| Eq |
θ=45°
等效重力加速度g′=
| F合 |
| m |
| 2 |
在等效重力场的“最高”点,小球刚好不掉下来时,由牛顿第二定律可得,
mg′=
| mv2 |
| R |
v=
| g′R |
从A到等效重力场的“最高”点,由动能定理
qE(L-Rsin45°)-mg(R+Rcos45°)=
| 1 |
| 2 |
L=
mg(1+
| ||||||||||||
| qE |
3
| ||
| 2 |
答:AB间的距离至少为(1+
3
| ||
| 2 |
点评:考查圆周运动最高点的最小速度,同时运用动能定理解题.
小球在混合场中的运动,关键分析清楚小球的受力的情况,找到小球在混合场中的最高点,在最高点时球的速度的大小是最小的.
小球在混合场中的运动,关键分析清楚小球的受力的情况,找到小球在混合场中的最高点,在最高点时球的速度的大小是最小的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,ABCDF为一绝缘光滑轨道,竖直放置在方向水平向右的匀强电场中,电场强度大小为E.AB面水平,BCDF是半径为R的圆形轨道,B为最低点.今有质量为m的带正电小球在电场力作用下由静止从A点开始沿轨道运动,小球受到的电场力和重力大小相等,小球能沿轨道做圆周运动到F点.
如图所示,ABCDF为一绝缘光滑轨道,竖直放置在方向水平向右的匀强电场中,电场强度大小为E.AB面水平,BCDF是半径为R的圆形轨道,B为最低点.今有质量为m的带正电小球在电场力作用下由静止从A点开始沿轨道运动,小球受到的电场力和重力大小相等,小球能沿轨道做圆周运动到F点.