题目内容
如图所示,长为L、电阻r=0.3 Ω、质量m=0.1 kg的金属棒CD垂直跨搁在位于水平面上的两条平行光滑金属导轨上,两导轨间距也是L,棒与导轨间接触良好,导轨电阻不计,导轨左端接有R=0.5 Ω的电阻,量程为0~3.0 A的电流表串接在一条导轨上,量程为0~1.0 V的电压表接在电阻R的两端,垂直导轨平面的匀强磁场向下穿过平面.现以向右恒定外力F使金属棒右移,当金属棒以v=2 m/s的速度在导轨平面上匀速滑动时,观察到电路中的一个电表正好满偏,而另一个电表未满偏,问:
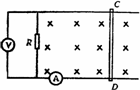
(1)此满偏的电表是什么表?说明理由.
(2)拉动金属棒的外力F多大?
(3)此时撤去外力F,金属棒将逐渐慢下来,最终停止在导轨上.求从撤去外力到金属棒停止运动的过程中通过电阻R的电量.
解析:
|
答案:(1)满偏的电表是电压表.因为若电流表满偏,电路中的电流I=3 A,电阻R两端的电压U=IR=1.5 V,已超过电压表量程. (2)外力拉动金属棒匀速右移时,外力的功率全部转化为电路中的电功率.根据功能关系有 而 (3)撤去外力F后,金属棒CD做减速运动,把金属棒减速至零的时间分成许多极短的时间间隔Δt1、Δt2、…、Δtn,在每一个极短的时间间隔内电流强度可以认为保持不变,大小分别为I1、I2、…、In,由动量定理可得金属棒在整个时间内的动量变化等于各段时间内所受安培力的冲量之和,即: 由电磁感应定律原来匀速右移的棒中产生的感应电动势 |
提示:
|
由两表的量程和电阻R的大小可判定哪一个表满偏;由功能关系即可求出外力F的大小;撤去外力后,感应电流大小不断变化,平均作用力的冲量BIL·Δt=BLq=m·Δv,变力作用下的导体运动问题可从电荷量的角度进行分析. |

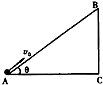 如图所示,长为L,倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q,质量为m的小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为v0,则( )
如图所示,长为L,倾角为θ的光滑绝缘斜面处于电场中,一带电量为+q,质量为m的小球,以初速度v0由斜面底端的A点开始沿斜面上滑,到达斜面顶端的速度仍为v0,则( )A、A、B两点的电势差一定为
| ||
| B、小球在B点的电势能一定大于小球在A点的电势能 | ||
C、若电场是匀强电场,则该电场的最小值一定是
| ||
| D、若该电场是斜面中点正上方某点的点电荷Q产生的,则Q一定是正电荷 |
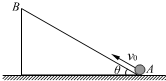 如图所示,长为L、倾角为θ的光滑绝缘斜面固定在水平面上,斜面处于电场中.一电荷量为+q、质量为m的小球以速度v0由斜面底端A沿斜面上滑,到达顶端B的速度仍为v0,则( )
如图所示,长为L、倾角为θ的光滑绝缘斜面固定在水平面上,斜面处于电场中.一电荷量为+q、质量为m的小球以速度v0由斜面底端A沿斜面上滑,到达顶端B的速度仍为v0,则( )A、若电场是匀强电场,则场强大小一定为
| ||
B、若电场是匀强电场,A、B两点间的电势差一定为
| ||
| C、不论电场是否是匀强电场,小球在B点的电势能一定大于在A点的电势能 | ||
D、不论电场是否是匀强电场,A、B两点间的电势差一定为
|
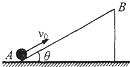 如图所示,长为L、倾角为θ的光滑绝缘斜面固定在水平面上,斜面处于电场中.有一质量为m、电荷量为+q的小球以速度v0由斜面底端A沿斜面上滑,到达顶端B的速度仍为v0,则( )
如图所示,长为L、倾角为θ的光滑绝缘斜面固定在水平面上,斜面处于电场中.有一质量为m、电荷量为+q的小球以速度v0由斜面底端A沿斜面上滑,到达顶端B的速度仍为v0,则( )| A、所加电场只能是匀强电场,小球做匀速直线运动 | ||
B、若电场是匀强电场,则场强大小的最小值为
| ||
| C、不论电场是否是匀强电场,电场力对电荷做功一定为mgLsinθ | ||
| D、不论电场是否是匀强电场,小球在B点的电势能一定大于在A点的电势能 |
 如图所示,长为L的金属导线弯成一圆环,导线的两端接在电容为C的平行板电容器上,P、Q为电容器的两个极板,磁场垂直于环面向里,磁感应强度以B=B0+Kt(K>0)随时间变化,t=0时,P、Q两板电势相等.两板间的距离远小于环的半径,经时间t,电容器P板带
如图所示,长为L的金属导线弯成一圆环,导线的两端接在电容为C的平行板电容器上,P、Q为电容器的两个极板,磁场垂直于环面向里,磁感应强度以B=B0+Kt(K>0)随时间变化,t=0时,P、Q两板电势相等.两板间的距离远小于环的半径,经时间t,电容器P板带 (2007?河东区模拟)如图所示,长为L,倾斜为θ的光滑绝缘斜面处于电场中.一带电量为+q,质量为m 的小球,以初速度vO由斜面底端的A 点开始沿斜面上滑,到达斜面顶端的速度仍为vO,则( )
(2007?河东区模拟)如图所示,长为L,倾斜为θ的光滑绝缘斜面处于电场中.一带电量为+q,质量为m 的小球,以初速度vO由斜面底端的A 点开始沿斜面上滑,到达斜面顶端的速度仍为vO,则( )