题目内容
平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动，在同一坐标系中做出两个分运动的v－t图线，如图所示，则以下说法不正确的是( )
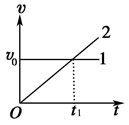
| A．图线1表示水平分运动的v－t图线 |
| B．图线2表示竖直分运动的v－t图线 |
| C．t1时刻物体的速度方向与初速度方向夹角为45° |
| D．若图线2倾角为θ，当地重力加速度为g，则一定有tanθ＝g |
D
试题分析：A、图线1表示表示匀速直线运动，所以图线1表示水平分运动的v－t图线；正确不选
B、图线2是初速度为0的匀加速直线运动，所以图线2表示的是竖直分运动；正确不选
C、
时刻可知水平分速度和竖直分速度相等，则速度与初速度方向的夹角为45°；正确不选D、若图线2斜率表示当地重力加速度，但是在v－t中，tanθ不一定等于图线的斜率；错误应选
故选D
点评：对于图线斜率，只有当坐标轴选用国际单位，且所选标度相同时，斜率才满足k=tanθ.
练习册系列答案
相关题目
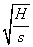v2
v2
v2
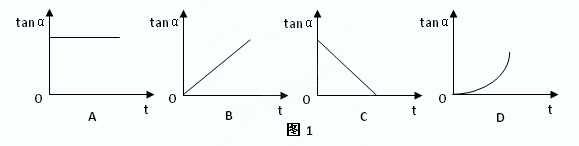
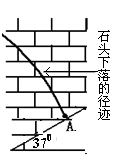
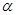的正切tanα随时间t变化的图像是图1中的：
