��Ŀ����
����Ŀ���⻬Բ���������бֱ��������ͼ��ʾװ�ã�����ֱ���bc�ֲڣ�ֱ���cd�⻬���������Ӵ�Ϊһ��С��Բ��������Ϊm=0.1kg�Ļ��飨����Ϊ�ʵ㣩��Բ�������Բ���˶�����������ߵ�aʱ���ٶȴ�СΪv=4m/s���������˶���Բ�����ֱ���bc�����д�bʱ������Բ�����ʼ����бֱ���bc���У�������cd�ϵ�d��ʱ�ٶ�Ϊ�㣮������任���˲���������ʧ�ɺ��Բ��ƣ���֪Բ����İ뾶ΪR=0.25m��ֱ���bc�������=37�����䳤��ΪL=26.25m��d����ˮƽ�����ĸ߶Ȳ�Ϊh=0.2m��ȡ�������ٶ�g=10m/s2��sin37��=0.6����
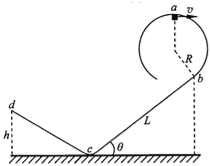
��1��������Բ�����ߵ�aʱ�Թ����ѹ����С��
��2��������ֱ���bc�ʵĶ�Ħ��������
��3��������ֱ���bc���ܹ��˶���ʱ�䣮
���𰸡���1��������Բ�����ߵ�aʱ�Թ����ѹ����С��5.4N��
��2��������ֱ���bc�ʵĶ�Ħ��������0.8��
��3��������ֱ���bc���ܹ��˶���ʱ����7.66s��
�������������������1����Բ�����ߵ�a�������ܵ������������֧�����ṩ����������ţ�ٵڶ����ɼ�����⣻
��2����a�㵽d��������Ħ����������ȫ���ɶ��ܶ���������⣻
��3���ֱ���ϻ��Ĺ��̺��»��Ĺ�����ʹ��ţ�ٵڶ����ɣ���ü��ٶȣ�Ȼ�����˶�ѧ�Ĺ�ʽ���������ʱ�䣮
�⣺��1����Բ�����ߵ�a���Ի�����ţ�ٵڶ����ɵã�![]()
����![]() =5.4N
=5.4N
��ţ�ٵ������ɵû�����Բ�����ߵ�aʱ�Թ����ѹ����СΪ5.4N
��2����a�㵽d��ȫ���ɶ��ܶ����ã�![]()
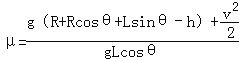 =0.8
=0.8
��3���軬����bc�����»����ļ��ٶ�Ϊa1��ʱ��Ϊt1�����ϻ����ļ��ٶ�Ϊa2��ʱ��Ϊt2����c��ʱ���ٶ�Ϊvc��
��c��d��![]()
![]() =2m/s
=2m/s
a�㵽b��Ĺ��̣�![]()
����![]() =5m/s
=5m/s
�ڹ��bc�ϣ�
�»���![]()
![]() =7.5s
=7.5s
�ϻ���mgsin��+��mgcos��=ma2
a2=gsin��+��gcos��=12.4m/s2
0=vc��a2t2
![]() =0.16s
=0.16s
��Ϊ����tan�������Ի����ڹ��bc��ֹͣ�����»�
����������б�����˶�����ʱ�䣺t��=t1+t2=��7.5+0.16��s=7.66s
�𣺣�1��������Բ�����ߵ�aʱ�Թ����ѹ����С��5.4N��
��2��������ֱ���bc�ʵĶ�Ħ��������0.8��
��3��������ֱ���bc���ܹ��˶���ʱ����7.66s��

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�