题目内容
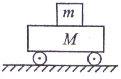 如图所示,小车质量M为2.0kg,它与水平地面摩擦力忽略不计,物体质量m为0.5kg,物体与小车间的动摩擦因数为0.3.求:
如图所示,小车质量M为2.0kg,它与水平地面摩擦力忽略不计,物体质量m为0.5kg,物体与小车间的动摩擦因数为0.3.求:
(1)小车在外力作用下以1.2m/s2的加速度向右运动时,物体受摩擦力多大?
(2)欲使小车产生a=3.5m/s2的加速度,需给小车提供多大的水平推力?
(3)若要使物体m脱离小车,则至少用多大的水平力推小车?
(4)若小车长L=1m,静止小车在8.5N水平推力的作用下,物体由车的右端向左滑动,则滑离小车需多长时间?(物体m看作质点)
解:(1)先求两者相对静止时的最大加速度am,当两物体间即将相对滑动时,摩擦力最大,对物体受力分析,由牛顿第二定律知,F合=μmg=mam,得到am=μg=3m/s2;
当a1=1.2m/s2时,物体与小车相对静止,对物体受力分析知,静摩擦力F1产生了加速度a1,由牛顿第二定律得F1=ma1,F1=0.6N.
(2)当a=3.5m/s2时,物体与小车发生了相对滑动,物体对小车的摩擦力大小为F=μmg=1.5N;
根据牛顿第三定律,物体对小车的摩擦力F′与小车对物体的摩擦力F大小相等;
对小车受力分析,由牛顿第二定律得F2-F′=Ma,得到F2=F′+Ma=8.5N;
故需给小车提供的推力为8.5N.
(3)要使物块m脱离小车,则必须有a车>a物,即a车>am ;
由牛顿第二定律得F3-F1=Ma车
解得 F3>(M+m)μg=7.5N;
故至少用7.5N的力推小车.
(4)由于F=8.5N,大于水平推力7.5N,所以物体会滑落,对小车受力分析,由牛顿第二定律:F-μmg=Ma4
物体的加速度 am=3m/s2;
物体m的位移 x1= amt2 ①
amt2 ①
小车的位移 x2= a4t2 ②
a4t2 ②
又因为x2-x1=L ③
联立①②③得运动时间t=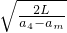 =2s;
=2s;
滑离小车需2s时间.
分析:(1)先求两者即将相对滑动的临界加速度,由于实际加速度小于临界加速度,故两物体相对静止,物体受摩擦力等于合力;
(2)实际加速度大于临界加速度,故两物体相对滑动,两物体间为滑动摩擦力,对小车受力分析,结合牛顿第二定律可求解;
(3)两物体即将相对滑动时,对两物体整体受力分析,结合牛顿第二定律可求出推力;
(4)分别对小车和物体受力分析,结合牛顿第二定律求出他们的加速度,再由位移时间公式和空间关系,可求出滑离时间.
点评:本题关键抓住两物体即将相对滑动的临界状态,求出临界加速度;同时要巧用整体法与隔离法对物体分析!
当a1=1.2m/s2时,物体与小车相对静止,对物体受力分析知,静摩擦力F1产生了加速度a1,由牛顿第二定律得F1=ma1,F1=0.6N.
(2)当a=3.5m/s2时,物体与小车发生了相对滑动,物体对小车的摩擦力大小为F=μmg=1.5N;
根据牛顿第三定律,物体对小车的摩擦力F′与小车对物体的摩擦力F大小相等;
对小车受力分析,由牛顿第二定律得F2-F′=Ma,得到F2=F′+Ma=8.5N;
故需给小车提供的推力为8.5N.
(3)要使物块m脱离小车,则必须有a车>a物,即a车>am ;
由牛顿第二定律得F3-F1=Ma车
解得 F3>(M+m)μg=7.5N;
故至少用7.5N的力推小车.
(4)由于F=8.5N,大于水平推力7.5N,所以物体会滑落,对小车受力分析,由牛顿第二定律:F-μmg=Ma4
物体的加速度 am=3m/s2;
物体m的位移 x1=
 amt2 ①
amt2 ①小车的位移 x2=
 a4t2 ②
a4t2 ②又因为x2-x1=L ③
联立①②③得运动时间t=
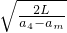 =2s;
=2s;滑离小车需2s时间.
分析:(1)先求两者即将相对滑动的临界加速度,由于实际加速度小于临界加速度,故两物体相对静止,物体受摩擦力等于合力;
(2)实际加速度大于临界加速度,故两物体相对滑动,两物体间为滑动摩擦力,对小车受力分析,结合牛顿第二定律可求解;
(3)两物体即将相对滑动时,对两物体整体受力分析,结合牛顿第二定律可求出推力;
(4)分别对小车和物体受力分析,结合牛顿第二定律求出他们的加速度,再由位移时间公式和空间关系,可求出滑离时间.
点评:本题关键抓住两物体即将相对滑动的临界状态,求出临界加速度;同时要巧用整体法与隔离法对物体分析!

练习册系列答案
相关题目
 如图所示,小车质量M为2.0kg,与水平地面阻力忽略不计,物体质量m为0.5kg,物体与小车间的动摩擦因数为0.3.求:
如图所示,小车质量M为2.0kg,与水平地面阻力忽略不计,物体质量m为0.5kg,物体与小车间的动摩擦因数为0.3.求: 如图所示,小车质量M为2.0kg,与水平地面阻力忽略不计,小物块质量m=0.50kg,小物块与小车间的动摩擦因数为0.3,则:(g=10m/s2)
如图所示,小车质量M为2.0kg,与水平地面阻力忽略不计,小物块质量m=0.50kg,小物块与小车间的动摩擦因数为0.3,则:(g=10m/s2) 如图所示,小车质量M=8kg,带电荷量q=+3×10-2C,置于光滑水平面上,水平面上方存在方向水平向右的匀强电场,场强大小E=2×102N/C.当小车向右的速度为3m/s时,将一个不带电、可视为质点的绝缘物块轻放在小车右端,物块质量m=1kg,物块与小车表面间动摩擦因数μ=0.2,小车足够长,g取10m/s2.求:
如图所示,小车质量M=8kg,带电荷量q=+3×10-2C,置于光滑水平面上,水平面上方存在方向水平向右的匀强电场,场强大小E=2×102N/C.当小车向右的速度为3m/s时,将一个不带电、可视为质点的绝缘物块轻放在小车右端,物块质量m=1kg,物块与小车表面间动摩擦因数μ=0.2,小车足够长,g取10m/s2.求: 如图所示,小车质量M=8㎏,带电荷量q=+3×10-2C,置于光滑水平面上,水平面上方存在方向水平向右的匀强电场,场强大小E=2×102N/C.当小车向右的速度为v=3m/s时,将一个不带电、可视为质点的绝缘物块轻放在小车右端,物块质量m=1kg,物块与小车表面间动摩擦因数μ=0.2,小车足够长,g取10m/s2,求:
如图所示,小车质量M=8㎏,带电荷量q=+3×10-2C,置于光滑水平面上,水平面上方存在方向水平向右的匀强电场,场强大小E=2×102N/C.当小车向右的速度为v=3m/s时,将一个不带电、可视为质点的绝缘物块轻放在小车右端,物块质量m=1kg,物块与小车表面间动摩擦因数μ=0.2,小车足够长,g取10m/s2,求: 如图所示,小车质量M为2.0kg,它与水平地面摩擦力忽略不计,物体质量m为0.5kg,物体与小车间的动摩擦因数为0.3.求:
如图所示,小车质量M为2.0kg,它与水平地面摩擦力忽略不计,物体质量m为0.5kg,物体与小车间的动摩擦因数为0.3.求: