��Ŀ����
����Ŀ����ͼ��ʾ�����ΪL������ƽ�Ƚ��������ɡ�L���Σ���ֱ��������ˮƽ��������㹻��������װ�ô�����ֱ���ϴ�СΪB����ǿ�ų��У�������Ϊm����ֵ��ΪR�ĵ����ab��cd����ֱ�ڵ�����ã���������뵼��䶯Ħ��������Ϊ�̣��������cd��ˮƽ�������������ٶ�v0��ˮƽ�������������˶�ʱ���ͷŵ����ab��������ֱ�������ȼ����»���ijʱ�̽������cd����ˮƽ������ȥ������һ��ʱ�䣬�����cd��ֹ���˹������������cd�ĵ����Ϊq�������ab��cd�뵼���Ӵ������ҽӴ��㼰��������ĵ��費�ƣ���֪�������ٶ�Ϊg������ ��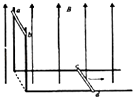
A.�����cd��ˮƽ��������ʱ�������ĵ���I= ![]()
B.�����ab�ȼ����»�ʱ�ļ��ٶȴ�Сa=g�� ![]()
C.�����cd��ˮƽ������ȥ������λ��Ϊs= ![]()
D.�����cd��ˮƽ������ȥ���������Ľ�����ΪQ= ![]() mv02��
mv02�� ![]()
���𰸡�B,C,D
���������⣺A��cd�и�Ÿ��߲�����Ӧ�綯��Ϊ E=BLv0�����ݱպϵ�·ŷķ���ɵã�I= ![]() =
= ![]() ����A����
����A����
B������ab������ţ�ٵڶ����ɵã�mg��f=ma��Ħ����f=��N��NΪ�����ab���ĵ�����ˮƽ������ƽ�������ã�N=BIL����ã�a=g�� ![]() ����B��ȷ��
����B��ȷ��
C������cd����ͨ�����ĵ�����q= ![]() =
= ![]() ����ã�s=
����ã�s= ![]() ����C��ȷ��
����C��ȷ��
D���赼���cd��ˮƽ������ȥ������Ľ�����ΪQ������ab�ĵ�����cd��ͬ�����ߴ�������ab�����Ľ�����ҲΪQ�����������غ�ã�2Q+��mgs= ![]() mv02����֪��s=
mv02����֪��s= ![]() ����ã�Q=
����ã�Q= ![]() mv02��
mv02�� ![]() ����D��ȷ��
����D��ȷ��
��ѡ��BCD��
cd�и�Ÿ��߲�����Ӧ�綯�ƣ���Ӧ�綯��Ϊ E=BLv0��abû���и�Ÿ��ߣ���������Ӧ�綯�ƣ����ݱպϵ�·ŷķ������õ����cd��ˮƽ��������ʱ�������ĵ���I������ţ�ٵڶ����ɺͰ�������ʽF=BIL���ab���ļ��ٶȴ�С�����ݸ�Ӧ������ʽq= ![]() ���s�����������غ㶨�����Q��
���s�����������غ㶨�����Q��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�