题目内容
2. 如图所示为一下粗上细且上端开口的薄壁玻璃管,管内有一部分水银封住密闭气体,上管足够长,图中大小截面积分别为S1=2cm2、S2=1cm2,粗细管内水银长度分别为h1=h2=2cm,封闭气体长度为L=22cm.大气压强为p0=76cmHg,气体初始温度为57℃.求:
如图所示为一下粗上细且上端开口的薄壁玻璃管,管内有一部分水银封住密闭气体,上管足够长,图中大小截面积分别为S1=2cm2、S2=1cm2,粗细管内水银长度分别为h1=h2=2cm,封闭气体长度为L=22cm.大气压强为p0=76cmHg,气体初始温度为57℃.求:①若缓慢降低气体温度,降低至多少开尔文时,所有水银全部进入粗管内;
②若温度降低至237K,气体的长度为多少.
分析 ①根据题意求出气体的状态参量,然后应用理想气体状态方程求出气体的温度;
②气体发生等压变化,应用盖吕萨克定律可以求出气体的体积,求出气柱的长度.
解答 解:①气体的状态参量:p1=p0+h1+h2=80cmHg,p2=p0+h1+$\frac{{h}_{2}}{2}$=79cmHg,
V1=LS1=22S1,V2=(L-$\frac{{h}_{2}{S}_{2}}{{S}_{1}}$)S1=(22cm-$\frac{2cm×1c{m}^{2}}{2c{m}^{2}}$)S1=21S1,T1=273+57=330K,
由理想气体状态方程得:$\frac{{p}_{1}{V}_{1}}{{T}_{1}}$=$\frac{{p}_{2}{V}_{2}}{{T}_{2}}$,代入数据解得:T2=311K;
②由于237K小于311K,所以再降温的过程中,气体将做等压变化,
气体状态参量:T3=273K,V3=L3S1,V2=21S1,
由盖吕萨克定律得:$\frac{{V}_{2}}{{T}_{2}}$=$\frac{{V}_{3}}{{T}_{3}}$,代入数据解得:L3=16cm;
答:①若缓慢降低气体温度,降低至311开尔文时,所有水银全部进入粗管内;
②若温度降低至237K,气体的长度为16cm.
点评 本题考查了求气体的温度、空气柱的长度,分析清楚气体状态变化过程是正确解题的前提与关键,求气体的状态参量,应用理想气体状态方程与盖吕萨克定律可以解题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
17.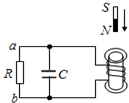 电阻R、电容C与一线圈连成闭合回路,条形磁铁静止于线圈的正上方,N极朝上,如图所示,现使磁铁由静止开始下落,在N极接近线圈上端的过程中,下列说法正确的是( )
电阻R、电容C与一线圈连成闭合回路,条形磁铁静止于线圈的正上方,N极朝上,如图所示,现使磁铁由静止开始下落,在N极接近线圈上端的过程中,下列说法正确的是( )
 电阻R、电容C与一线圈连成闭合回路,条形磁铁静止于线圈的正上方,N极朝上,如图所示,现使磁铁由静止开始下落,在N极接近线圈上端的过程中,下列说法正确的是( )
电阻R、电容C与一线圈连成闭合回路,条形磁铁静止于线圈的正上方,N极朝上,如图所示,现使磁铁由静止开始下落,在N极接近线圈上端的过程中,下列说法正确的是( )| A. | 流过R的电流方向是a到b | B. | 电容器的下极板带正电 | ||
| C. | 磁铁下落过程中,加速度保持不变 | D. | 穿过线圈的磁通量不断增大 |
14. 如图所示,质量分别为m1和m2两个物体用两根轻质细线,分别悬挂在天花板上的A、B两点,两线与水平方向夹角分别为α,β且α>β,两物体间的轻质弹簧恰好处于水平状态,两根绳子拉力分别为TA和TB,则下列说法正确的是( )
如图所示,质量分别为m1和m2两个物体用两根轻质细线,分别悬挂在天花板上的A、B两点,两线与水平方向夹角分别为α,β且α>β,两物体间的轻质弹簧恰好处于水平状态,两根绳子拉力分别为TA和TB,则下列说法正确的是( )
 如图所示,质量分别为m1和m2两个物体用两根轻质细线,分别悬挂在天花板上的A、B两点,两线与水平方向夹角分别为α,β且α>β,两物体间的轻质弹簧恰好处于水平状态,两根绳子拉力分别为TA和TB,则下列说法正确的是( )
如图所示,质量分别为m1和m2两个物体用两根轻质细线,分别悬挂在天花板上的A、B两点,两线与水平方向夹角分别为α,β且α>β,两物体间的轻质弹簧恰好处于水平状态,两根绳子拉力分别为TA和TB,则下列说法正确的是( )| A. | TA=TB | B. | TA<TB | C. | m1=m2 | D. | m1>m2 |
11.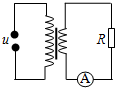 如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )
 如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )
如图所示,理想变压器原、副线圈的匝数比是10:1,原线圈输入交变电压u=100$\sqrt{2}$sin50πt(V),在副线圈中接有理想电流表和定值电阻R,电阻阻值R=10Ω,关于电路分析,下列说法中正确的是( )| A. | 交流电的频率为50Hz | |
| B. | 电流表示数是$\sqrt{2}$A | |
| C. | 电阻R消耗的电功率为10W | |
| D. | 若用电容器替代电阻R,则该电容器的耐压值至少是10V |
11.如图甲为简谱横波在t=0时刻的波形图象,图乙为横波中x=6m处质点P的振动图象,则下列说法正确的是( )


| A. | 波的传播方向沿x轴负方向 | |
| B. | 波的传播方向沿x轴正方向 | |
| C. | 波的传播速度大小为2m/s | |
| D. | 在t=9s时刻,图甲中质点P的振动速度最大 | |
| E. | 在t=1s时刻与t=0时刻相比,x=5m处质点的加速度方向相反 |
