题目内容
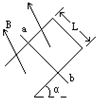 如图所示,U形导体框架宽L=1m,与水平面成α=30°角倾斜放置在匀强磁场中,磁感应强度B=0.2T,垂直框面向上.在框架上垂直框边放有一根质量m=0.2kg、有效电阻R=0.1Ω的导体棒ab,从静止起沿框架无摩擦下滑,设框架电阻不计,框边有足够长,取g=10m/s2,求:ab棒下滑的最大速度vm.
如图所示,U形导体框架宽L=1m,与水平面成α=30°角倾斜放置在匀强磁场中,磁感应强度B=0.2T,垂直框面向上.在框架上垂直框边放有一根质量m=0.2kg、有效电阻R=0.1Ω的导体棒ab,从静止起沿框架无摩擦下滑,设框架电阻不计,框边有足够长,取g=10m/s2,求:ab棒下滑的最大速度vm.分析:导体棒ab向下先做加速度减小的加速运动,后做匀速运动,速度达到最大,此时棒受到重力、支持力、滑动摩擦力、安培力平衡,推导出安培力与速度关系式,由平衡条件求出最大速度vm.
解答:解:导体棒ab向下先做加速度减小的加速运动,后做匀速运动,速度达到最大,由匀速运动的力平衡条件得:
mgsinα=FA
又FA=BIL,I=
则得:FA=
联立得:vm=
=
m/s=2.5m/s
答:ab棒下滑的最大速度vm为2.5m/s.
mgsinα=FA
又FA=BIL,I=
| BLvm |
| R |
则得:FA=
| B2L2vm |
| R |
联立得:vm=
| mgRsinα |
| B2L2 |
| 0.2×10×0.1×0.5 |
| 0.2×0.2×1×1 |
答:ab棒下滑的最大速度vm为2.5m/s.
点评:本题是电磁感应与力学知识的综合题,推导出安培力与速度的关系式是关键,再根据导体棒的运动状态,运用平衡条件进行研究是常用的思路,也可以根据能量守恒定律求解.

练习册系列答案
相关题目
 (2004?江苏)如图所示,U形导线框MNQP水平放置在磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为0.5m,横跨在导线框上的导体棒ab的电阻r=1.0Ω,接在NQ间的电阻R=4.OΩ,电压表为理想电表,其余电阻不计.若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦.
(2004?江苏)如图所示,U形导线框MNQP水平放置在磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为0.5m,横跨在导线框上的导体棒ab的电阻r=1.0Ω,接在NQ间的电阻R=4.OΩ,电压表为理想电表,其余电阻不计.若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦.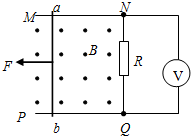 如图所示,U形导线框MNQP水平放置在 磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为L=0.5m,横跨在导线框上的导体棒ab的质量m=0.1kg,电阻r=1.0Ω,接在NQ间的电阻R=4.0Ω,电压表为理想电表,其余电阻不计.若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦.求:
如图所示,U形导线框MNQP水平放置在 磁感应强度B=0.2T的匀强磁场中,磁感线方向与导线框所在平面垂直,导线MN和PQ足够长,间距为L=0.5m,横跨在导线框上的导体棒ab的质量m=0.1kg,电阻r=1.0Ω,接在NQ间的电阻R=4.0Ω,电压表为理想电表,其余电阻不计.若导体棒在水平外力作用下以速度ν=2.0m/s向左做匀速直线运动,不计导体棒与导线框间的摩擦.求:
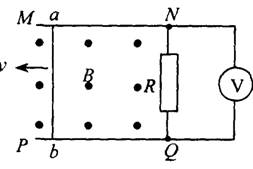 (1)通过电阻及的电流方向如何?
(1)通过电阻及的电流方向如何?