题目内容
(2013?江苏一模)如图甲所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰好与两个固定在地面上的压力传感器X和Y相接触.图中AB高H=0.3m、AD长L=0.5m,斜面倾角θ=37°.可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数μ可以通过更换斜面表面的材料进行调节(调节范围是0≤μ≤1).sin 37°=0.6,cos 37°=0.8,重力加速度取g=10m/
.
(1)令μ=0,将P由D点静止释放,求P在斜面上的运动时间;
(2)令μ=0.5,在A点给P一个沿斜面向上的初速度
=2m/s,求P落地时的动能;
(3)将X和Y接到同一数据处理器上,已知当X和Y受到物块压力时,分别显示正值和负值.对于不同的μ,每次都在D点给P一个沿斜面向下足够大的初速度以保证它能滑离斜面,求滑行过程中处理器显示的读数F随μ变化的关系表达式,并在乙图坐标系中画出其函数图象.
| s | 2 |

(1)令μ=0,将P由D点静止释放,求P在斜面上的运动时间;
(2)令μ=0.5,在A点给P一个沿斜面向上的初速度
| v | 0 |
(3)将X和Y接到同一数据处理器上,已知当X和Y受到物块压力时,分别显示正值和负值.对于不同的μ,每次都在D点给P一个沿斜面向下足够大的初速度以保证它能滑离斜面,求滑行过程中处理器显示的读数F随μ变化的关系表达式,并在乙图坐标系中画出其函数图象.
分析:(1)根据牛顿第二定律求出加速度的大小,结合位移时间公式求出运动的时间.
(2)根据动能定理求出P上滑到速度为零时经历的位移,对全过程运用动能定理,求出P落地时的动能.
(3)对梯形物块受力分析,结合共点力平衡得出F与P与斜面动摩擦因数的关系式,从而作出其图线.
(2)根据动能定理求出P上滑到速度为零时经历的位移,对全过程运用动能定理,求出P落地时的动能.
(3)对梯形物块受力分析,结合共点力平衡得出F与P与斜面动摩擦因数的关系式,从而作出其图线.
解答:解:(1)当μ=0时,P沿斜面下滑的加速度为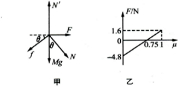
a=gsinθ=6m/s2
由运动学规律L=
at2,
得t=
,代入数据解得t=
s
(2)设P沿斜面上滑的位移为s时速度为零.
由动能定理:-(mgsinθ+μmgcosθ)s=0-
mv02
代入数据解得s=0.2m.
设落地时P的动能为Ek,则
由动能定理得,mgH-μmgcosθ?2s=Ek-
mv02
代入数据解得Ek=3.4J.
(3)P在斜面上下滑的过程中物块受力如图甲所示,由平衡条件可得F+Nsinθ=fcosθ
将N=mgcosθ和f=μmgcosθ代入得,F=mgcosθ(μcosθ-sinθ)
代入数据得,F=6.4μ-4.8,其图象如乙图.
答:(1)P在斜面上的运动时间为
s.
(2)P落地时的动能为3.4J.
(3)图线如图所示.

a=gsinθ=6m/s2
由运动学规律L=
| 1 |
| 2 |
得t=
|
| ||
| 6 |
(2)设P沿斜面上滑的位移为s时速度为零.
由动能定理:-(mgsinθ+μmgcosθ)s=0-
| 1 |
| 2 |
代入数据解得s=0.2m.
设落地时P的动能为Ek,则
由动能定理得,mgH-μmgcosθ?2s=Ek-
| 1 |
| 2 |
代入数据解得Ek=3.4J.
(3)P在斜面上下滑的过程中物块受力如图甲所示,由平衡条件可得F+Nsinθ=fcosθ
将N=mgcosθ和f=μmgcosθ代入得,F=mgcosθ(μcosθ-sinθ)
代入数据得,F=6.4μ-4.8,其图象如乙图.
答:(1)P在斜面上的运动时间为
| ||
| 6 |
(2)P落地时的动能为3.4J.
(3)图线如图所示.
点评:本题综合考查了牛顿第二定律、动能定理以及运动学公式,综合性较强,对学生的能力要求较高,需加强这方面的训练.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 (2013?江苏一模)如图所示,质量为
(2013?江苏一模)如图所示,质量为 (2013?江苏一模)如图所示,小物块在竖直平面内的拉力F作用下沿倾角为θ的斜面向下运动,若重力做的功与克服拉力F做的功相等.则( )
(2013?江苏一模)如图所示,小物块在竖直平面内的拉力F作用下沿倾角为θ的斜面向下运动,若重力做的功与克服拉力F做的功相等.则( ) (2013?江苏一模)如图所示是一列简谐横波在t=0时的波形图,此时P点沿y轴的正方向运动,已知波的传播速度为2m/s.则该波沿
(2013?江苏一模)如图所示是一列简谐横波在t=0时的波形图,此时P点沿y轴的正方向运动,已知波的传播速度为2m/s.则该波沿 (2013?江苏一模)如图所示,一比荷为
(2013?江苏一模)如图所示,一比荷为