题目内容
6.水平方向的匀强磁场高度为d,A、B为两个电阻相同且宽度均为d的单匝闭合导线框,它们的长度LA=$\frac{d}{2}$,LB=$\frac{3}{2}$d.绕制线圈的导线粗细相同,材料密度之比为ρA:ρB=5:3.两个线圈在距离磁场上界相同高度处由静止开始自由下落,若下落过程中磁场力始终小于线框的重力,线圈从开始下落到进入磁场$\frac{d}{2}$的过程中产生的热量为QA和QB,线圈在通过磁场时无感应电流的时间分别为tA、tB;下列判断正确的是( )
| A. | QA>QB tA>tB | B. | QA<QB tB<tA | C. | QA=QB tB<tA | D. | QA=QB tB=tA |
分析 根据牛顿第二定律和密度公式分析两个线框进入磁场时加速度关系,判断速度关系,再由焦耳定律分析焦耳热关系.当穿过线框的磁通量不变时没有感应电流产生.
解答 解:据题可知,两个线圈在距离磁场上界相同高度处由静止开始自由下落,进入磁场时的速度相同.
线框进入磁场后,根据牛顿第二定律得:
对A线框:mAg-$\frac{{B}^{2}{d}^{2}v}{{R}_{A}}$=mAaA;得:aA=g-$\frac{{B}^{2}{d}^{2}v}{{m}_{A}{R}_{A}}$=g-$\frac{{B}^{2}{d}^{2}v}{{ρ}_{A}•3dS•{R}_{A}}$
对B线框:mBg-$\frac{{B}^{2}{d}^{2}v}{{R}_{B}}$=mBaB;得:aB=g-$\frac{{B}^{2}{d}^{2}v}{{m}_{B}{R}_{B}}$=g-$\frac{{B}^{2}{d}^{2}v}{{ρ}_{B}•5dS•{R}_{B}}$
据题知:RA=RB,3ρA=5ρB,所以得到:aA=aB.
说明两个线框进入后运动情况相同,从开始下落到进入磁场$\frac{d}{2}$的过程所用时间相同,由E=Bdv知两个线框同一时刻产生的感应电动势相等,感应电流相等,由焦耳定律可知产生热量相等,即有QA=QB.
当穿过线框的磁通量不变时没有感应电流产生,A完全在磁场中运动时,没有感应电流,通过位移大小为$\frac{d}{2}$,B没有感应电流的过程通过的位移也是$\frac{d}{2}$,由于A刚没有感应电流时的初速度较小,所以所用时间较长,即有tB<tA.
故选:C.
点评 本题关键要综合考虑影响加速度的因素,将加速度表达式中质量和电阻细化,从而分析两线框的关系.

练习册系列答案
相关题目
14. 某同学在一次实验中利用速度传感器与计算机结合,得到的运动小车的速度-时间图象如图所示,由图可知( )
某同学在一次实验中利用速度传感器与计算机结合,得到的运动小车的速度-时间图象如图所示,由图可知( )
 某同学在一次实验中利用速度传感器与计算机结合,得到的运动小车的速度-时间图象如图所示,由图可知( )
某同学在一次实验中利用速度传感器与计算机结合,得到的运动小车的速度-时间图象如图所示,由图可知( )| A. | 小车先做匀加速运动,后做匀减速运动 | |
| B. | 小车运动的最大速度约为0.8m/s | |
| C. | 小车的最大位移在数值上等于图象中曲线与t轴所围的面积 | |
| D. | 小车做曲线运动 |
14.关于加速度的概念,下列说法正确的是( )
| A. | 加速度就是增加出来的速度 | |
| B. | 加速度方向一定与速度变化量的方向相同 | |
| C. | 加速度的大小反映了速度变化的快慢 | |
| D. | 物体有加速度,速度不一定增大 | |
| E. | $\frac{△v}{△t}$叫速度变化率,就是加速度 |
15.以初速度v0水平抛出一物体,当竖直位移与水平位移相等时( )
| A. | 竖直分速度等于水平分速度 | B. | 瞬时速度为$\sqrt{5}$v0 | ||
| C. | 运动时间为$\frac{2{v}_{0}}{g}$ | D. | 速度的方向与水平方向成45° |
16. 如图,轻弹簧直立在地面上.一个物体从弹簧正上方高处自由落下.在A处,物体与弹簧接触.在B处,物体受合力为零( )
如图,轻弹簧直立在地面上.一个物体从弹簧正上方高处自由落下.在A处,物体与弹簧接触.在B处,物体受合力为零( )
 如图,轻弹簧直立在地面上.一个物体从弹簧正上方高处自由落下.在A处,物体与弹簧接触.在B处,物体受合力为零( )
如图,轻弹簧直立在地面上.一个物体从弹簧正上方高处自由落下.在A处,物体与弹簧接触.在B处,物体受合力为零( )| A. | 物体从A到B这段过程中作匀加速运动 | |
| B. | 物体从A到B这段过程中,速度先减小后增大 | |
| C. | 物体到达B处时,速度为零 | |
| D. | 物体到达B处时,动能达到最大 |
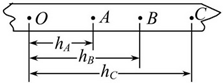 某个小组的三位同学按照正确的操作选得纸带如图.其中O是起始点,A、B、C是打点计时器连续打下的3个点.该同学用毫米刻度尺测量O到A、B、C各点的距离,用重锤在OB段的运动来验证机械能守恒,已知当地的重力加速度g=9.80m/s2,打点计时器所用电源频率为f=50Hz,设重锤质量为1.00kg.
某个小组的三位同学按照正确的操作选得纸带如图.其中O是起始点,A、B、C是打点计时器连续打下的3个点.该同学用毫米刻度尺测量O到A、B、C各点的距离,用重锤在OB段的运动来验证机械能守恒,已知当地的重力加速度g=9.80m/s2,打点计时器所用电源频率为f=50Hz,设重锤质量为1.00kg.