题目内容
7.某同学利用图(a)所示实验装置及数字化信息系统获得了小车加速度a与钩码的质量m的对应关系图.如图(b)所示.实验中小车(含发射器)的质量为200g,实验时选择了不可伸长的轻质细绳和轻定滑轮,小车的加速度由位移传感器及与之相连的计算机得到.回答下列问题:(1)根据该同学的结果,小车的加速度与钩码的质量成非线性(填“线性”或“非线性”)关系.
(2)由图(b)可知,a-m图线不经过原点,可能的原因是存在存在摩擦力.
(3)若利用本实验装置来验证“在小车质量不变的情况下,小车的加速度与作用力成正比”的结论,并直接以钩码所受重力mg作为小车受到的合外力,则实脸中应采取的改进措施是调节轨道的倾斜度以平衡摩擦力,钩码的质量应满足的条件是远小于小车的质量.

分析 该实验的研究对象是小车,采用控制变量法研究.当质量一定时,研究小车的加速度和小车所受合力的关系.为消除摩擦力对实验的影响,可以把木板的右端适当垫高,以使小车的重力沿斜面分力和摩擦力抵消,那么小车的合力就是绳子的拉力.
解答 解:(1)根据该同学的结果得出a-m图线是曲线,即小车的加速度与钩码的质量成非线性关系;
(2)从上图中发现直线没过原点,当a=0时,m≠0,即F≠0,也就是说当绳子上拉力不为0时,小车的加速度为0,所以可能的原因是存在摩擦力.
(3)若利用本实验来验证“小车质量不变的情况下,小车的加速度与作用力成正比”的结论,并直接以钩码所受重力mg作为小车受到的合外力,则实验中应采取的改进措施是:
①调节轨道的倾斜度以平衡摩擦力,即使得绳子上拉力等于小车的合力.
②根据牛顿第二定律得,整体的加速度a=$\frac{mg}{M+m}$,则绳子的拉力F=Ma=$\frac{mg}{1+\frac{m}{M}}$,知钩码的质量远小于小车的质量时,绳子的拉力等于钩码的重力,所以钩码的质量应满足的条件是远小于小车的质量.
故答案为:(1)非线性;(2)存在摩擦力;(3)调节轨道的倾斜度以平衡摩擦力;远小于小车的质量.
点评 该实验是探究加速度与力、质量的三者关系,研究三者关系必须运用控制变量法.
对于实验我们要清楚每一项操作存在的理由.比如为什么要平衡摩擦力,这样问题我们要从实验原理和减少实验误差方面去解决.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
18.试判断下面的几个速度中是瞬时速度是( )
| A. | 物体在第1秒内的速度是4m/s | |
| B. | 物体在第2秒末的速度是4m/s | |
| C. | 物体在通过其路径上某一点的速度是4m/s | |
| D. | 物体在通过某一段位移时的速度是4m/s |
2.做匀加速直线运动的物体,依此通过ABC三点,位移XAB=XBC.已知物体在AB段的平均速度大小为3.0m/s,在BC段的平均速度大小为6.0m/s,则物体在B点瞬时速度的大小是( )
| A. | 4.0m/s | B. | 4.5m/s | C. | 5.0m/s | D. | 5.5m/s |
12.飞机起飞时,其竖直方向速度随时间变化规律如图所示,下列说法正确的是( )


| A. | 飞机经20min达到最高点 | B. | 飞机飞行的最大高度为4500m | ||
| C. | 飞机经5min达到最高点 | D. | 飞机飞行的最大高度为6000m |
19.枪管呈水平状态对准小球,枪口与小球之间的距离为100m,当子弹射出枪口时,小球恰好开始自由落下.小球落下0.2s时被子弹击中,则子弹离开枪口时的速度为(取g=10m/s2)( )
| A. | 200m/s | B. | 300m/s | C. | 400m/s | D. | 500m/s |
16.如图所示电路中,L为电感线圈,线圈电阻不计,A、B为两灯泡,则不正确的是( )
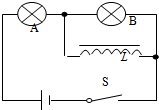

| A. | 合上S时,A先亮,B后亮 | B. | 合上S时,A、B同时亮起来 | ||
| C. | 合上S过一会儿后,A继续亮,B熄灭 | D. | 断开S时,A熄灭,B闪亮一下再熄灭 |
17.质量为m的物体,在距地面h高处以$\frac{g}{3}$的加速度由静止竖直下落到地面,下列说法中错误的是( )
| A. | 重力做功mgh | B. | 物体的机械能减少$\frac{2mgh}{3}$ | ||
| C. | 物体的动能增加$\frac{mgh}{3}$ | D. | 物体的重力势能减少$\frac{mgh}{3}$ |
 质量为m的物体放在摩擦系数为μ的水平面上.在t=0的时刻,一个与时间成正比(比例系数为A)、与水平成角θ的力F开始作用在此物体上,求经过ts后物体的速度v.
质量为m的物体放在摩擦系数为μ的水平面上.在t=0的时刻,一个与时间成正比(比例系数为A)、与水平成角θ的力F开始作用在此物体上,求经过ts后物体的速度v.