��Ŀ����
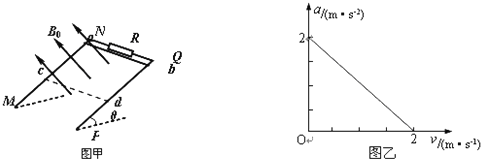
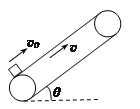
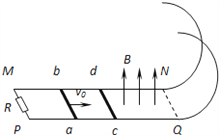
����Ŀ����ͼ��ʾ����Ϊ![]() ��MN��PQ��ƽ�й⻬ˮƽ����ֱ���뾶
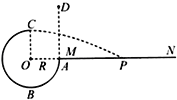
��MN��PQ��ƽ�й⻬ˮƽ����ֱ���뾶![]() ����ͬ��ֱ��Բ������N��Q��ƽ�����ӣ�M��P�����Ӷ�ֵ����R������
����ͬ��ֱ��Բ������N��Q��ƽ�����ӣ�M��P�����Ӷ�ֵ����R������![]() ��cd��Ե�˴�ֱ��ֹ��ˮƽ�����ϣ������Ҳ���N��Q�˵������ڳ�����ֱ���ϵ���ǿ�ų���
��cd��Ե�˴�ֱ��ֹ��ˮƽ�����ϣ������Ҳ���N��Q�˵������ڳ�����ֱ���ϵ���ǿ�ų��� ![]() ��������
��������![]() ��ab�����ˣ�����Ϊ
��ab�����ˣ�����Ϊ![]() �����Գ��ٶ�
�����Գ��ٶ�![]() ˮƽ������cd��Ե�˷�����������ų�������δ������cd��Ե����ǡ����ͨ����Բ������ߵ㣬�������������Ħ����ab������ʼ���뵼�촹ֱ�ҽӴ����ã�ȡ
ˮƽ������cd��Ե�˷�����������ų�������δ������cd��Ե����ǡ����ͨ����Բ������ߵ㣬�������������Ħ����ab������ʼ���뵼�촹ֱ�ҽӴ����ã�ȡ![]() ����
����
��1������˲��cd��Ե�˵��ٶȴ�С![]() ��ab�������ٶȴ�С
��ab�������ٶȴ�С![]() ��
��
��2������ab�����˽���ų�˲���ܵ��İ�������С![]() ��
��
��3��![]() �����˽���ų��˶�ȫ�����У���·�����Ľ�����Q��
�����˽���ų��˶�ȫ�����У���·�����Ľ�����Q��
���𰸡���1���ֱ�Ϊ![]() ��
��![]() ����2��0.01N��3��2J
����2��0.01N��3��2J
��������![]() ��Ե��ͨ����Բ������ߵ�ʱ����ţ�ٵڶ������У�
��Ե��ͨ����Բ������ߵ�ʱ����ţ�ٵڶ������У� ![]()
��ã� ![]()
��ײ��cd��Ե�˻�����ߵ�Ĺ����У��ɶ��ܶ����У� ![]()
�����ײ��cd��Ե�˵��ٶȣ� ![]()
������ײ���̣������غ㣬����ٶȷ���Ϊ���������У� ![]()
�����ײ��ab�����˵��ٶȣ� ![]()
![]() �����˽���ų�˲�䣬�ɷ����ڵ�Ÿ�Ӧ���ɣ�
�����˽���ų�˲�䣬�ɷ����ڵ�Ÿ�Ӧ���ɣ� ![]()
�պϵ�·ŷķ���ɣ� ![]()
��������ʽ�� ![]()
������ã� ![]() N
N![]() ��
��
![]() �����˽���ų����������غ㶨���У�
�����˽���ų����������غ㶨���У� ![]()
��ã� ![]() J
J![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�