题目内容
【题目】如图所示,竖直平面内四分之一光滑圆弧轨道AP和水平传送带PC相切于P点,某同学让一质量为m=5kg的物块甲从圆弧顶点A由静止开始沿轨道下滑,滑到P时，与静止在轨道低端的质量M=1kg的物快乙相碰并粘在一起，两物块滑行到传送带右端恰好与传送带速度相同，且均为
。已知两物块与传送带间的滑动摩擦因数为μ=0.1，圆弧轨道半径为R=1.8m,重力加速度为g=10m/
,物快甲乙均视为质点，则（ ）
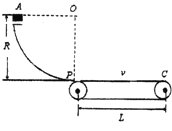
A. 传送带长度为4.5m
B. 物块甲与乙碰撞前瞬间对轨道的压力大小为100N
C. 物块甲和乙滑上传送带时的速度大小为6m/s
D. 物块甲和乙在传送带上滑行的过程中产生的热量为3J
【答案】AD
【解析】
传送带沿逆时针方向转动时，物体在传送带上受到的滑动摩擦力与转速无关，运动情况不变。从A到C对小物块运用动能定理列式，可求得PC之间的距离L；若传送带速度大小v0不变，顺时针转动，先由动能定理求出物块到达P点的速度。分析物块滑上传送带后的运动情况，由牛顿第二定律和运动学公式求物块从P点滑到C点所用的时间t。
A、C项：物块甲从A到P由动能定理可得：
，解得：
甲、乙两物体碰撞由动量守恒得：
，解得：
甲、乙粘在一起从P到C由公式
解得：L=4.5m，故A正确，C错误；
B项：在P点对物块甲由牛顿第二定律可得：
，解得：N=150N，故B错误；
D项：甲、乙粘在一起从P到C所用的时间为：
，热量Q=
，故D正确。
故应选：AD。
练习册系列答案
名校课堂系列答案
相关题目
