题目内容
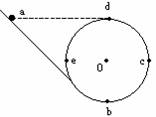
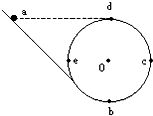 一个竖直放置的光滑圆环,半径为R,c、e、b、d分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图所示.一个小球从与d点高度相等的a点从斜轨上无初速下滑.试求:
一个竖直放置的光滑圆环,半径为R,c、e、b、d分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图所示.一个小球从与d点高度相等的a点从斜轨上无初速下滑.试求:(1)过b点时,对轨道的压力Nb多大?
(2)小球能否过d点,如能,在d点对轨道压力Nd多大?如不能,小球于何处离开圆环?
分析:(1)从a运动到b点的过程中机械能守恒,根据机械能守恒定律求出到达b点的速度,在b点根据向心力公式列式即可求解;
(2)先根据机械能守恒定律判断小球能不能到达d点,若不能,则小球做斜抛运动,根据机械能守恒定律及几何关系结合向心力公式即可求解从何处脱离轨道.
(2)先根据机械能守恒定律判断小球能不能到达d点,若不能,则小球做斜抛运动,根据机械能守恒定律及几何关系结合向心力公式即可求解从何处脱离轨道.
解答: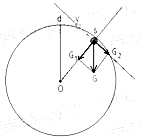 解:(1)因为从a运动到b点的过程中机械能守恒,
解:(1)因为从a运动到b点的过程中机械能守恒,
则 mgha=
m
解得:
=2gha=4gR
在b点,根据向心力公式得:
Nb-G=m
解得:Nb=mg+m
=mg+m
=5mg
(2)小球如能沿圆环内壁滑动到d点,表明小球在d点仍在做圆周运动,则Nd+G=m
由上式可见,G是恒量,随着vd的减小,Nd减小;
当Nd已经减小到零(表示小球刚能到d点,但球与环顶已是接触而无挤压,处于“若即若离”状态)时,vd=
是能过d点的最小速度.如小球速度低于这个速度,
就不可能沿圆环到达d点.这就表明小球如能到达d点,其机械能至少应是
Ed=mghd+
m
但是,小球在a点出发的机械能仅有Ea=mgha=mghd<Ed
因此小球不可能到达d点.
由于hc=
ha,Ea=Ed
所以mgha=mghc+
m
因此,vc>0,即小球从b滑到c点时仍有沿切线向上的速度,所以小球一定是在c、d之间的某点s离开圆环的.设半径Os与竖直方向夹α角,
则由图可见,小球高度hs=(1+cosα)R
根据机械能守恒定律小球到达S点的速度VS应符合:
mgha=mghs+
m
=2g(ha-hs)
所以
=2gR(1-cosα)①
小球从s点开始脱离圆环,所以圆环对小球已无弹力,仅由重力G
沿半径方向的分力G1提供向心力,即F心=G1=mgcosα,亦即mgcosα=m
②
将①式代入②式得 mgcosα=2mg(1-cosα)
cosα=
所以hs=(1+cosα)?R=
R
所以,小球到达高度为
R的s点开始脱离圆环,做斜上抛运动.
答:(1)过b点时,对轨道的压力Nb为5mg;(2)小球能不能过d点,小球到达高度为
R的s点开始脱离圆环,做斜上抛运动.
 解:(1)因为从a运动到b点的过程中机械能守恒,
解:(1)因为从a运动到b点的过程中机械能守恒,则 mgha=
| 1 |
| 2 |
| v | 2 b |
解得:
| v | 2 b |
在b点,根据向心力公式得:
Nb-G=m
| vb2 |
| R |
解得:Nb=mg+m
| ||
| R |
| 4gR |
| R |
(2)小球如能沿圆环内壁滑动到d点,表明小球在d点仍在做圆周运动,则Nd+G=m
| vd2 |
| R |
由上式可见,G是恒量,随着vd的减小,Nd减小;
当Nd已经减小到零(表示小球刚能到d点,但球与环顶已是接触而无挤压,处于“若即若离”状态)时,vd=
| gR |
就不可能沿圆环到达d点.这就表明小球如能到达d点,其机械能至少应是
Ed=mghd+
| 1 |
| 2 |
| v | 2 d |
但是,小球在a点出发的机械能仅有Ea=mgha=mghd<Ed
因此小球不可能到达d点.
由于hc=
| 1 |
| 2 |
所以mgha=mghc+
| 1 |
| 2 |
| v | 2 c |
因此,vc>0,即小球从b滑到c点时仍有沿切线向上的速度,所以小球一定是在c、d之间的某点s离开圆环的.设半径Os与竖直方向夹α角,
则由图可见,小球高度hs=(1+cosα)R
根据机械能守恒定律小球到达S点的速度VS应符合:
mgha=mghs+
| 1 |
| 2 |
| v | 2 s |
| v | 2 s |
所以
| v | 2 s |
小球从s点开始脱离圆环,所以圆环对小球已无弹力,仅由重力G
沿半径方向的分力G1提供向心力,即F心=G1=mgcosα,亦即mgcosα=m
| vs2 |
| R |
将①式代入②式得 mgcosα=2mg(1-cosα)
cosα=
| 2 |
| 3 |
所以hs=(1+cosα)?R=
| 5 |
| 3 |
所以,小球到达高度为
| 5 |
| 3 |
答:(1)过b点时,对轨道的压力Nb为5mg;(2)小球能不能过d点,小球到达高度为
| 5 |
| 3 |
点评:本题主要考查了机械能守恒定律、向心力公式的直接应用,要求同学们学会判断能否到达最高点的方法并能结合几何关系求解,难度较大.

练习册系列答案
相关题目
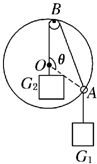 如图所示,光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上,今有一细绳拴在小圆环A上,另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码,如果不计小环、滑轮、绳子的重量大小.绳子又不可伸长,求平衡时弦AB所对的圆心角θ的一半的正弦值,即sin
如图所示,光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上,今有一细绳拴在小圆环A上,另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码,如果不计小环、滑轮、绳子的重量大小.绳子又不可伸长,求平衡时弦AB所对的圆心角θ的一半的正弦值,即sin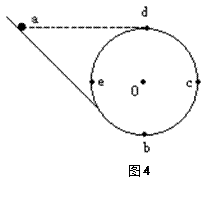 小球能否过
小球能否过