题目内容
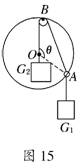
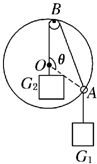如图所示，光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上，今有一细绳拴在小圆环A上，另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码，如果不计小环、滑轮、绳子的重量大小．绳子又不可伸长，求平衡时弦AB所对的圆心角θ的一半的正弦值，即sin| θ | 2 |
分析：选取小圆环A为研究对象，画受力分析示意图，小圆环受三个力，两个绳子的拉力和大圆环的支持力，一定要知道大圆环的支持力只能是沿着半径的，由此两端绳子拉力分别在切线方向上的分力必然相等，然后由数学三角函数知识求解
解答：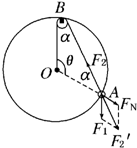
解：以小圆环A为研究对象，它受到的力有：竖直绳对它的拉力
F1=G1，其方向竖直向下；AB绳对它的拉力F2=G2，其方向沿AB方向；
大圆环对它的弹力FN，其方向沿半径指向圆外，在F1、F2、FN三力的共同作用下，
小圆环处于平衡状态．
将小圆环A所受的三个力利用力的合成和力的分解，组成三角形，如图所示．
由几何关系得△OAB与△FNAF2′相似，得
=
=
所以FN=F1，sin
=
将F1=G1、F2=G2代入
解得sin
=
．
答：
的正弦值为
．
解：以小圆环A为研究对象，它受到的力有：竖直绳对它的拉力F1=G1，其方向竖直向下；AB绳对它的拉力F2=G2，其方向沿AB方向；
大圆环对它的弹力FN，其方向沿半径指向圆外，在F1、F2、FN三力的共同作用下，
小圆环处于平衡状态．
将小圆环A所受的三个力利用力的合成和力的分解，组成三角形，如图所示．
由几何关系得△OAB与△FNAF2′相似，得
| OA |
| FN |
| OB |
| F1 |
| AB |
| F2′ |
所以FN=F1，sin
| θ |
| 2 |
| ||
| F1 |
将F1=G1、F2=G2代入
解得sin
| θ |
| 2 |
| G2 |
| 2G1 |
答：
| θ |
| 2 |
| G2 |
| 2G1 |
点评：本题主要考查了平行四边形进行力的合成的方法，另外要重视数学计算在物理中的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
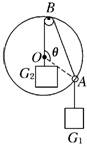如图所示，光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上，今有一细绳拴在小圆环A上，另一端跨过固定在大圆环最高点B处的一个光滑小滑轮后吊着一个重为G2的砝码，不计小环、滑轮和绳子的质量，绳子又不可伸长，平衡时弦AB所对的圆心角为θ，则下列关系正确的是（ ）| A、G2=2G1sinθ | ||
B、G1=2G2sin
| ||
C、G2=2G1sin
| ||
D、G2=2G1cos
|
