题目内容
【题目】如图所示，半径为l、质量为m的小球用两根不可伸长的轻绳a、b连接，两轻绳的另一端系在一根竖直杆的A、B两点上，A、B两点相距为l，当两轻绳伸直后，A、B两点到球心的距离均为l．当竖直杆以自己为轴转动并达到稳定时（细绳a、b与杆在同一竖直平面内）．求：计算结果可以带根号，g不要带具体值．
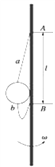
（1）竖直杆角速度ω为多大时，小球恰离开竖直杆．
（2）ω至少达到多少时b轻绳伸直开始有拉力．
【答案】
【解析】试题分析：小球恰离开竖直杆时，受重力和拉力，拉力的竖直分力与重力平衡，水平分力提供向心力；角速度ω再增大，轻绳b拉直后，小球做圆周运动，再根据拉力的竖直分力与重力平衡，水平分力提供向心力列式求解。
（1）小球恰离开竖直杆时，小球与竖直杆间的作用力为零，此时轻绳a与竖直杆间的角为α，由题意可知：
，半径为：
沿半径方向：
垂直半径方向：
联立解得：
（2）角速度ω再增大，轻绳b拉直后，小球做圆周运动的半径为
沿半径方向：
垂直半径方向：
联立解得：
练习册系列答案
相关题目
【题目】“验证力的平行四边形定则”的实验情况如图甲所示，其中A为固定橡皮筋的图钉，O为橡皮筋与细绳的结点，OB和OC为细绳，图乙是在白纸上根据实验结果画出的图。
（1）本实验采用的科学方法是
A．理想实验法 | B．等效替代法 |
C．控制变量法 | D．建立物理模型法 |
（2）某同学用两个弹簧秤将结点拉至某位置，此时该同学记录下了结点O的位置以及两弹簧秤对应的读数，他还应该记录下_____________。
（3）图乙中的F是利用平行四边形定则作出的两个弹簧拉力的合力的图示，
为用一个弹簧秤将结点拉至同一点时所用拉力的图示，这两个力中，方向一定沿AO方向的是__________。
