题目内容
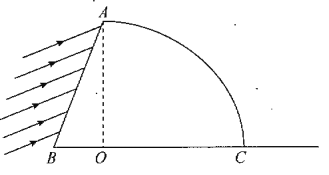
【题目】如图所示，为一水平放置在桌面上的玻璃砖的截面图，其中右侧为半径为r的
圆AOC，O为圆心，左侧为直角三角形ABO，∠B=60°，玻璃砖折射率n=
。一束平行于纸面的光以60°的入射角射到AB边上，忽略玻璃砖AB、BC内表面光的反射，光在真空中的传播速度为c。求∶
（i）桌面上C点右侧有光照亮区域的长度；
（ii）玻璃砖中刚好透射不出的光线，从AB面进入到AC弧面的传播时间。
【答案】（i）
；（ii）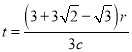
。
【解析】
（i）光线在AB面上的折射角为
可得
θ=30°
即光线垂直于AO即平行于BC射到AC面上；若某条光线在圆弧内表面恰未发全反射，则其到达桌面上的位置D与C点相距最远，即桌面上CD之间的区域被照亮。设临界角为C，则
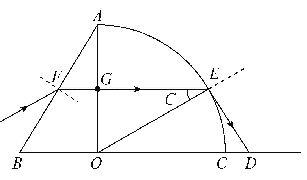
由几何关系得
CD=OD-r
解得
（ii）由几何关系得
，
故光在玻璃中的传播距离
设光在玻璃中的传播速度为n，则
传播时间
解得
练习册系列答案
相关题目
