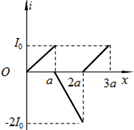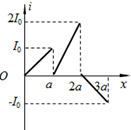题目内容
20. 如图所示,半径为r的圆柱形转筒,绕其竖直中心轴OO′转动,小物体a在圆筒的内壁上,它与圆筒间的动摩擦因数为μ,要使小物体不下落,圆筒转动的角速度至少为( )
如图所示,半径为r的圆柱形转筒,绕其竖直中心轴OO′转动,小物体a在圆筒的内壁上,它与圆筒间的动摩擦因数为μ,要使小物体不下落,圆筒转动的角速度至少为( )| A. | $\sqrt{\frac{μg}{r}}$ | B. | $\sqrt{μg}$ | C. | $\sqrt{\frac{g}{r}}$ | D. | $\sqrt{\frac{g}{μr}}$ |
分析 要使物体不下落,筒壁对物体的静摩擦力必须与重力相平衡,由筒壁对物体的支持力提供向心力,根据向心力公式即可求解角速度的最小值.
解答 解:要使物体不下落,则小物块在竖直方向上受力平衡,有:f=mg
当摩擦力正好等于最大摩擦力时,圆筒转动的角速度ω取最小值,筒壁对物体的支持力提供向心力,根据向心力公式得:
N=mω2r
而f=μN
联立以上三式解得:ω=$\sqrt{\frac{g}{μr}}$.
故选:D.
点评 物体在圆筒内壁做匀速圆周运动,向心力是由筒壁对物体的支持力提供的.而物体放在圆盘上随着圆盘做匀速圆周运动时,此时的向心力是由圆盘的静摩擦力提供的.

练习册系列答案
相关题目
10.假设地球同步卫星的轨道半径是地球半径的n倍,则( )
| A. | 同步卫星运行速度是第一宇宙速度的$\frac{1}{n}$倍 | |
| B. | 同步卫星的运行速度是第一宇宙速的$\sqrt{\frac{1}{n}}$倍 | |
| C. | 同步卫星的运行速度是地球赤道上物体随地球自转速度的$\frac{1}{n}$倍 | |
| D. | 同步卫星的向心加速度是地球表面重力加速度的$\frac{1}{n}$倍 |
11. 光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )
光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )
 光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )
光滑绝缘曲面与竖直平面的交线是抛物线,如图所示,抛物线的方程是y=x2,下半部处在一个水平方向的匀强磁场中,磁场的上边界是y=a的直线(图中的虚线所示),一个质量为m的小金属球从抛物线上y=b(b>a)处沿抛物线自由下滑,忽略空气阻力,重力加速度值为g.则( )| A. | 小金属球沿抛物线下滑后最终停在O点 | |
| B. | 小金属球沿抛物线下滑后每次过O点速度一直在减小 | |
| C. | 小金属球沿抛物线下滑后对O点压力一定大于mg | |
| D. | 小金属球沿抛物线下滑后最终产生的焦耳热总量是mg(b-a) |
8.如图所示,A、B是相同的白炽灯,L是自感系数很大、电阻可忽略的自感线圈.下面说法正确的是( )


| A. | 闭合开关S时,A、B灯同时亮,且达到正常 | |
| B. | 闭合开关S时,B灯比A灯先亮,最后一样亮 | |
| C. | 闭合开关S时,A灯比B灯先亮,最后一样亮 | |
| D. | 断开开关S时,A、B灯同时熄灭 |
15. 如图所示,小钢球m以初速度v0在光滑水平面上运动,后受到磁极的侧向作用力而作图示的曲线运动到达D点,由图可知磁极的位置及极性可能是( )
如图所示,小钢球m以初速度v0在光滑水平面上运动,后受到磁极的侧向作用力而作图示的曲线运动到达D点,由图可知磁极的位置及极性可能是( )
 如图所示,小钢球m以初速度v0在光滑水平面上运动,后受到磁极的侧向作用力而作图示的曲线运动到达D点,由图可知磁极的位置及极性可能是( )
如图所示,小钢球m以初速度v0在光滑水平面上运动,后受到磁极的侧向作用力而作图示的曲线运动到达D点,由图可知磁极的位置及极性可能是( )| A. | 磁极在A位置,极性一定是N极 | B. | 磁极在B位置,极性一定是S极 | ||
| C. | 磁极在C位置,极性一定是N极 | D. | 磁极在B位置,极性无法确定 |
12.质量为m的物体受到一组共点恒力作用而处于平衡状态,当撤去某个恒力F1时,物体不可能做( )
| A. | 匀加速直线运动 | B. | 匀减速直线运动 | C. | 匀变速曲线运动 | D. | 匀速直线运动 |
 如图所示,已知某人骑自行车每分钟蹬30圈,车轮与脚蹬轮盘转数之比为4:1,车轮半径为0.50m,则求车轮转动的线速度为6.28m/s.
如图所示,已知某人骑自行车每分钟蹬30圈,车轮与脚蹬轮盘转数之比为4:1,车轮半径为0.50m,则求车轮转动的线速度为6.28m/s.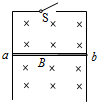 如图所示,竖直平面内有间距l=40cm、足够长的平行直导轨,导轨上端连接一开关S.长度恰好等于导轨间距的导体棒ab与导轨接触良好且无摩擦,导体棒ab的电阻R=0.40Ω,质量m=0.20kg.导轨电阻不计,整个装置处于与导轨平面垂直的水平匀强磁场中,磁场的磁感强度B=0.50T,方向垂直纸面向里.空气阻力可忽略不计,取重力加速度g=10m/s2.
如图所示,竖直平面内有间距l=40cm、足够长的平行直导轨,导轨上端连接一开关S.长度恰好等于导轨间距的导体棒ab与导轨接触良好且无摩擦,导体棒ab的电阻R=0.40Ω,质量m=0.20kg.导轨电阻不计,整个装置处于与导轨平面垂直的水平匀强磁场中,磁场的磁感强度B=0.50T,方向垂直纸面向里.空气阻力可忽略不计,取重力加速度g=10m/s2. 如图所示,有两个相邻的有界匀强磁场区域,磁感应强度的大小均为B,磁场方向相反,且与纸面垂直,磁场区域在x轴方向宽度均为a,在y轴方向足够宽.现有一高为a的正三角形导线框从图示位置开始向右匀速穿过磁场区域.若以逆时针方向为电流的正方向,在下图中,线框中感应电流i与线框移动距离x的关系图象正确的是( )
如图所示,有两个相邻的有界匀强磁场区域,磁感应强度的大小均为B,磁场方向相反,且与纸面垂直,磁场区域在x轴方向宽度均为a,在y轴方向足够宽.现有一高为a的正三角形导线框从图示位置开始向右匀速穿过磁场区域.若以逆时针方向为电流的正方向,在下图中,线框中感应电流i与线框移动距离x的关系图象正确的是( )