题目内容
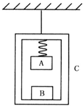 如图所示,A、B是两相同的木块,C木箱,A、C间用轻质弹簧相连,木箱C用轻绳悬挂在天花板上,A、B、C最均为m.现剪断轻绳,则在剪断轻绳的瞬间,A、B、C的加速度分别为( )
如图所示,A、B是两相同的木块,C木箱,A、C间用轻质弹簧相连,木箱C用轻绳悬挂在天花板上,A、B、C最均为m.现剪断轻绳,则在剪断轻绳的瞬间,A、B、C的加速度分别为( )分析:弹簧的弹力不能突变,因形变需要过程,绳的弹力可以突变,绳断拉力立即为零先对A受力分析,求出细线剪短前后A的加速度;若BC之间有弹力,则可以把BC看成一个整体,对B、C整体受力分析,求出BC整体的加速度,隔离B,求出B的加速度,比较两者关系判断BC间是否存在弹力,再根据牛顿第二定律即可求解.
解答:解:剪断轻绳的瞬间,A受到重力和弹簧的弹力都不发生改变,处于平衡状态,加速度为零,
若BC之间有弹力,则可以把BC看成一个整体,受到重力2mg,弹簧的拉力mg,根据牛顿第二定律可知,整体加速度a=
=1.5mg,对B进行受力分析,B受到重力和向上的支持力,合力必然小于mg,则加速度也小于g,与题设矛盾,所以BC间没有弹力,故B只受重力,加速度为g,C受到重力和弹簧向下的拉力,根据牛顿第二定律得:ac=
=2g,故B正确.
故选:B.
若BC之间有弹力,则可以把BC看成一个整体,受到重力2mg,弹簧的拉力mg,根据牛顿第二定律可知,整体加速度a=
| 3mg |
| 2m |
| 2mg |
| m |
故选:B.
点评:考查了牛顿第二定律,绳和弹簧弹力的特点,瞬时对应关系,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,a、b是两个带有同种电荷的小球,现用两根绝缘细线将它们悬挂于真空中同一点.已知两球静止时,它们离水平地面的高度相等,线与竖直方向的夹角分别为α、β,且α<β.现有以下判断,其中正确的是( )
如图所示,a、b是两个带有同种电荷的小球,现用两根绝缘细线将它们悬挂于真空中同一点.已知两球静止时,它们离水平地面的高度相等,线与竖直方向的夹角分别为α、β,且α<β.现有以下判断,其中正确的是( ) 电风扇的扇叶的重心如果不在转轴上,转动时会使风扇抖动,并加速转轴磨损.调整时,可在扇叶的一区域通过固定小金属块的办法改变其重心位置.如图所示,A、B是两调整重心的金属块(可视为质点),其质量相等,它们到转轴O的距离rA<rB.扇叶转动后,它们的( )
电风扇的扇叶的重心如果不在转轴上,转动时会使风扇抖动,并加速转轴磨损.调整时,可在扇叶的一区域通过固定小金属块的办法改变其重心位置.如图所示,A、B是两调整重心的金属块(可视为质点),其质量相等,它们到转轴O的距离rA<rB.扇叶转动后,它们的( )| A、向心力FA<FB | B、线速度大小相等 | C、向心加速度相等 | D、角速度大小相等 |
 如图所示,A、B是两块相同的均匀长方形砖块,质量为M,长度L,叠放在一起,且A相对于B的右端伸出
如图所示,A、B是两块相同的均匀长方形砖块,质量为M,长度L,叠放在一起,且A相对于B的右端伸出 (2011?锦州模拟)如图所示,A、B是两个位于固定斜面上的正方体物块,它们的质量相等,F是沿水平方向作用于A上的外力,已知A与B的接触面,A、B与斜面的接触面均光滑,下列说法正确的是( )
(2011?锦州模拟)如图所示,A、B是两个位于固定斜面上的正方体物块,它们的质量相等,F是沿水平方向作用于A上的外力,已知A与B的接触面,A、B与斜面的接触面均光滑,下列说法正确的是( ) 如图所示,A,B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键K闭合时,下列说法正确的是( )
如图所示,A,B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键K闭合时,下列说法正确的是( )