题目内容
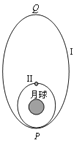
【题目】半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的3/4倍.将珠子从环上最低位置A点静止释放,则:

(1)珠子所能获得的最大动能是多少?
(2)珠子对圆环的最大压力是多少?
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】(1)如图,在珠子能够静止的一点进行受力分析;设OB与OA之间的夹角为θ,则:![]()
所以:θ=37°,珠子在等效最低点B时具有最大的动能.

珠子从A到B的过程电场力和重力做功,珠子的动能增加,即:
﹣mgr(1﹣cosθ)+qErsinθ=EK﹣0
解得珠子所能获得的最大动能:Ek=﹣mgr(1﹣cosθ)+qErsinθ=![]() .
.
(2)珠子在最低点B处受到的压力最大.
根据合力提供向心力![]()
又因为重力和电场力的合力F=![]() ,
,![]()
所以![]()
根据牛顿第三定律,珠子对圆环的最大压力是![]() .
.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目