题目内容
1.两相邻匀强磁场区域的磁感应强度大小不同,方向平行.一速度方向与磁感应强度方向垂直的带电粒子(不计重力),从较强磁场区域进入到较弱区域后,粒子的( )| A. | 轨道半径减小,角速度增大 | B. | 轨道半径减小,角速度减小 | ||
| C. | 轨道半径增大,角速度增大 | D. | 轨道半径增大,角速度减小 |
分析 通过洛伦兹力提供向心力得知轨道半径的公式,结合该公式即可得知进入到较弱磁场区域后时,半径的变化情况;再利用线速度与角速度半径之间的关系式,即可得知进入弱磁场区域后角速度的变化情况.
解答 解:带电粒子在匀强磁场中做匀速圆周运动,洛伦兹力提高向心力,由牛顿第二定律有:qvB=m$\frac{{v}^{2}}{r}$,
解得:r=$\frac{mv}{qB}$,
从较强磁场区域进入到较弱磁场区域后.B减小,所以r增大.线速度、角速度的关系为:v=ωR
线速度v不变,半径r增大,所以角速度减小,故D正确,ABC错误.
故选:D.
点评 本题考查了粒子在磁场中的运动,解答该题要明确洛伦兹力始终不做功,洛伦兹力只是改变带电粒子的运动方向,应用牛顿第二定律、线速度与角速度的关系即可解题.

练习册系列答案
相关题目
11.如图甲为一列简谐波沿x轴传播的波形图,若从图示时刻开始计时,那么图乙可表示( )
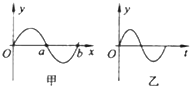

| A. | 当波沿x轴正方向传播时,图乙表示a质点的振动图象 | |
| B. | 当波沿x轴负方向传播时,图乙表示a质点的振动图象 | |
| C. | 当波沿x轴正方向传播时,图乙表示b质点的振动图象 | |
| D. | 当波沿x轴负方向传播时,图乙表示b质点的振动图象 |
6.关于电动势,下列说法正确的是( )
| A. | 电源两极间的电压等于电源电动势 | |
| B. | 电动势越大的电源,将其他形式的能转化为电能的本领越大 | |
| C. | 电源电动势的数值等于内、外电压之和 | |
| D. | 电源电动势与外电路的组成无关 |
13.如图所示,物块在水平圆盘上,与圆盘一起绕固定轴匀速运动,下列说法中正确的是( )


| A. | 物块处于平衡状态 | |
| B. | 物块受二个力作用 | |
| C. | 在角速度一定时,物块到转轴的距离越远,物块越容易脱离圆盘 | |
| D. | 在物块到转轴距离一定时,物块运动周期越小,越容易脱离圆盘 |

 如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T.一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离P的距离应为1m (g取10m/s2)
如图所示,水平传送带以恒定速度5m/s沿图示方向运动,地面上PQ区间有垂直纸面向里的匀强磁场,B=1T.一质量为0.01kg的带正电0.05C的小物体从磁场左方某处无初速释放到传送带上,若物体与传送带间的动摩擦因数μ=0.2,那么,欲使小物体能匀速通过磁场区域,它释放时离P的距离应为1m (g取10m/s2) 如图所示,用50cm的细线将质量为2×10-3kg的带电小球P悬挂在O点下,当空中有方向为水平向左,大小为5×104N/C的匀强电时,小球偏转45°后处于静止状态.(g=10m/s2)
如图所示,用50cm的细线将质量为2×10-3kg的带电小球P悬挂在O点下,当空中有方向为水平向左,大小为5×104N/C的匀强电时,小球偏转45°后处于静止状态.(g=10m/s2)