题目内容
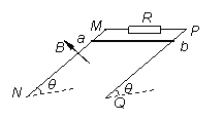
【题目】如图所示,光滑的长平行金属导轨宽度为L,导轨所在的平面与水平面夹角为θ,导轨上端电阻阻值为R,其他电阻不计,导轨放在垂直斜面向上的匀强磁场中,磁感应强度大小为B。质量为m的金属棒ab从上端由静止开始下滑,(![]() )
)
(1)若L=50cm,![]() ,R=0.8Ω,B=0.4T,m=0.1kg,
,R=0.8Ω,B=0.4T,m=0.1kg,
①求导体棒下滑的最大速度![]() ;
;
② 当速度达到6m/s时导体棒的加速度a;
(2)若经过时间t,导体棒下滑的距离为s,速度为v,若在同一时间内,电阻R产生的热与一交变电流在该电阻上产生的热相同,求该交变电流有效值![]() 的表达式 (各物理量全部用字母表示)
的表达式 (各物理量全部用字母表示)
(3)若导体棒从静止开始运动到速度稳定过程中,导体杆下滑的距离为![]() ,到达稳定的速度大小为
,到达稳定的速度大小为![]() ,求导体棒从静止到刚刚达到稳定速度所经历的时间
,求导体棒从静止到刚刚达到稳定速度所经历的时间![]() 的表达式(各物理量全部用字母表示)
的表达式(各物理量全部用字母表示)
【答案】(1)12 ,3(2)![]() (3)
(3)![]()
【解析】试题分析:(1)①由安培力公式求出安培力,然后由平衡条件求出最大速度;②由安培力公式求出安培力,由牛顿第二定律求出加速度;(2)由能量守恒定律与焦耳定律分析答题。(3)根据电量的表达式![]() 和动量定理求解时间。
和动量定理求解时间。
(1)①导体棒速度最大时做匀速直线运动,导体棒受到的安培力:![]()
导体棒做匀速直线运动,处于平衡状态,由平衡条件得:![]()
解得:![]()
②由牛顿第二定律得:![]()
已知:v=6m/s,代入数据解得:![]()
(2)由能量守恒定律得:![]()
由焦耳定律得:![]()
解得:![]()
(3)导体棒从静止开始运动到速度稳定过程中,产生的电量为![]()
由动量定理得:![]() ,又
,又![]()
联立解得:![]()

【题目】两年以来,物理组的最高领导一直在考驾照,今天又和前(N+8)次一样,早早地来到客运站,思考到达考点的三种途径。第一种是乘普客汽车国道到达;第二种方法是乘快客汽车经高速公路到达;第三种方法是乘火车到达;下面是三种车的发车时刻及里程表,已知普客汽车全程平均时速度为60km/h,快客汽车全程平均时速为100km/h,两车途中均不停站,火车在中途需停靠石台站5min,设火车进站和出站都做匀变速直线运动,加速度大小是2400km/h2,途中匀速行驶,速率为120km/h,若现在时刻是上午8点05分,科目二开考时间是9点25分,请你通过计算说明他能否赶上考试?如果能,该选择乘哪个班次什么车?(单位统一用km/h)
普客汽车 | 快客汽车 | 火车 | |
里程/km | 75 | 80 | 72 |
班次 | 7∶20 8∶20 10∶30 14∶30 …… | 8∶00 8∶40 9∶20 10∶55 …… | 8∶00 8∶33 9∶00 9∶43 …… |