ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥»Υ…ηΦΤΝΥ»γΆΦΥυ ΨΒΡΜ§ΑεΗω–‘Μ§ΒάΓΘ–±ΟφAB”κΑκΨΕRΘΫ3 mΒΡΙβΜ§‘≤ΜΓΙλΒάBCœύ«–”ΎBΘ§‘≤ΜΓΕ‘”ΠΒΡ‘≤–ΡΫ«Π»ΘΫ37Γψ«“ΙΐCΒψΒΡ«–œΏΥ°ΤΫΘ§CΒψΝ§Ϋ”«ψΫ«ΠΝΘΫ30ΓψΒΡ–±ΟφCDΓΘ“ΜΜ§ΑεΑ°ΚΟ’ΏΝ§Ά§Μ§ΑεΒ»ΉΑ±Η( ”ΈΣ÷ Βψ)Ήή÷ ΝΩmΘΫ60 kgΓΘΡ≥¥Έ ‘Μ§Θ§Υϊ¥”–±Οφ…œΡ≥ΒψP”…Ψ≤÷ΙΩΣ Φœ¬Μ§Θ§ΖΔœ÷‘Ύ–±ΟφCD…œΒΡ¬δΒψQ«ΓΚΟάκCΒψΉν‘ΕΓΘ»τΥϊ‘Ύ–±ΟφAB…œΜ§Ε·Ιΐ≥Χ÷–Υυ ήΡΠ≤ΝΝΠFf”κΈΜ“Τ¥σ–ΓxΒΡΙΊœΒ¬ζΉψFfΘΫ90x(Ψυ≤…”ΟΙζΦ ÷ΤΒΞΈΜ)Θ§Κω¬‘Ω’ΤχΉηΝΠΘ§»ΓgΘΫ10 m/s2Θ§sin 37ΓψΘΫ0.6Θ§cos 37ΓψΘΫ0.8ΓΘ«σΘΚ
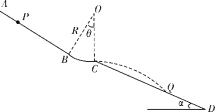
(1)PΓΔBΝΫΒψΦδΒΡΨύάκΘΜ
(2)Μ§Αε‘ΎCΒψΕ‘ΙλΒάΒΡ―ΙΝΠ¥σ–ΓΓΘ
ΓΨ¥πΑΗΓΩΘ®1Θ©4mΘ®2Θ©1320 N
ΓΨΫβΈωΓΩ
(1)…ηΑ°ΚΟ’ΏΜ§ΒΫCΒΡΥΌΕ»ΈΣvCΘ§Υ°ΤΫΓΔ ζ÷±ΖΫœρΒΡΈΜ“ΤΖ÷±πΈΣx1ΓΔy1
CΒΫQ”…ΤΫ≈Ή‘ΥΕ·Ιφ¬…”–ΘΚ![]() ΓΓ ΔΌ
ΓΓ ΔΌ
‘ρ![]() ΓΓΔΎ
ΓΓΔΎ
“ρ¥Υ![]() ΓΓΔέ
ΓΓΔέ
![]() ΓΓΔή
ΓΓΔή
”…Δή ΫΩ…÷ΣvC‘Ϋ¥σ‘ρ![]() ΦδΨύ‘Ϋ¥σΘ§”…»ΥΚΆΉΑ±Η‘ΎBCΦδ‘ΥΕ· ±Μζ–ΒΡή ΊΚψΩ…÷ΣΘ§“Σ ΙvC‘Ϋ¥σΨΆ“Σ«σvB‘Ϋ¥σΓΘ
ΦδΨύ‘Ϋ¥σΘ§”…»ΥΚΆΉΑ±Η‘ΎBCΦδ‘ΥΕ· ±Μζ–ΒΡή ΊΚψΩ…÷ΣΘ§“Σ ΙvC‘Ϋ¥σΨΆ“Σ«σvB‘Ϋ¥σΓΘ
…η–±ΟφABΒΡ«ψΫ«ΈΣΠ»Θ§»ΥΚΆΉΑ±Η‘ΎPΓΔBΦδ‘ΥΕ· ±Φ”ΥΌΕ»ΈΣaΘ§”…≈ΘΕΌΒΎΕΰΕ®¬…
”–![]() ΓΓΔί
ΓΓΔί
ΒΟ![]() ΓΓΔό
ΓΓΔό
”…Δό ΫΩ…÷ΣΘΚ»ΥΚΆΉΑ±ΗΉωΦ”ΥΌΕ»Φθ–ΓΒΡΦ”ΥΌ÷±œΏ‘ΥΕ·Θ§Β±Φ”ΥΌΕ»ΈΣΝψ ±ΥΌΕ»vBΉν¥σΓΘ
Φ¥PΓΔBΝΫΒψΦδΒΡΨύάκ¥σ–ΓΈΣΘΚ![]() ΔΏΘΜ
ΔΏΘΜ
(2)…ηPΓΔBΦδΡΠ≤ΝΝΠΕ‘»ΥΉωΙΠΈΣ![]() Θ§”…Ε·ΡήΕ®άμ”–ΘΚ
Θ§”…Ε·ΡήΕ®άμ”–ΘΚ![]() ΓΓΔύ
ΓΓΔύ
Εχ![]() ΓΓΔα
ΓΓΔα
(Μρ”…ΔύΔαΒΟ![]() )
)
BΓΔCΦδ‘ΥΕ·Μζ–ΒΡή ΊΚψ![]() Δβ
Δβ
‘ΎCΒψ![]()
ΫβΒΟ![]()
(Τδ÷–![]() Θ§
Θ§![]() )
)
”…≈ΘΕΌΒΎ»ΐΕ®¬…Ω…÷ΣΜ§Αε‘ΎCΒψΕ‘ΙλΒάΒΡ―ΙΝΠ¥σ–Γ![]() ΓΘ
ΓΘ