��Ŀ����
����Ŀ�����ٶȴ�СΪv�����Ӻ����ֹ��﮺ˣ� ![]() Li���������˷�Ӧ������밺˺ͦ����ӣ����ɵ�밺��ٶȷ��������ӵij��ٶȷ����෴��밺�������ӵ��ٶ�֮��Ϊ7��8�����ӵ�����Ϊm�����ӵ������ɽ��ƿ���m������Ϊc��
Li���������˷�Ӧ������밺˺ͦ����ӣ����ɵ�밺��ٶȷ��������ӵij��ٶȷ����෴��밺�������ӵ��ٶ�֮��Ϊ7��8�����ӵ�����Ϊm�����ӵ������ɽ��ƿ���m������Ϊc��
��1��д���˷�Ӧ���̣�
��2����밺˺ͦ����ӵ��ٶȴ�С��
��3�����˷�Ӧ�����зų��ĺ���ȫ��ת��Ϊ�����Ӻ�밺˵Ķ��ܣ������������
���𰸡�
��1���⣺���������������غ㣬���У� ![]() n+
n+ ![]() Li����
Li���� ![]() H+
H+ ![]() He
He
�𣺺˷�Ӧ���� ![]() n+
n+ ![]() Li����
Li���� ![]() H+
H+ ![]() He
He
��2���⣺�ɶ����غ㶨�ɵ�mnv=��mHv1+mHev2��
�������v1��v2=7��8
��ã�v1= ![]() v��v2=
v��v2= ![]() v
v
��밺˺ͦ����ӵ��ٶȴ�С�ֱ�Ϊ��v1= ![]() v��v2=
v��v2= ![]() v
v
��3���⣺밺˺ͦ����ӵĶ���֮��Ϊ
Ek= ![]() ��3mv
��3mv ![]() +
+ ![]() ��4mv
��4mv ![]() =
= ![]() mv2
mv2
�ͷŵĺ���Ϊ
��E=Ek��Ekn= ![]() mv2��
mv2�� ![]() mv2=
mv2= ![]() mv2��
mv2��
�ɰ���˹̹���ܷ��̵ã���������Ϊ
��m= ![]() =
= ![]()
������������ ![]()
����������1�������������͵�����غ㣬��д�˷�Ӧ���̣���2�����ݶ����غ㶨����⺤�˵��ٶȣ���3��������������ٸ��ݰ���˹̹���ܷ������˷�Ӧ�ͷų���������
�����㾫����������Ŀ����֪���������ö����غ㶨�ɺ����ܷ��̵����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��䣻����˹̹�������ָ�������������������֮����������е���ϵ�����ǵĹ�ϵ�ǣ�E = mc2������ǰ���˹̹�����ܷ��̣�

 ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
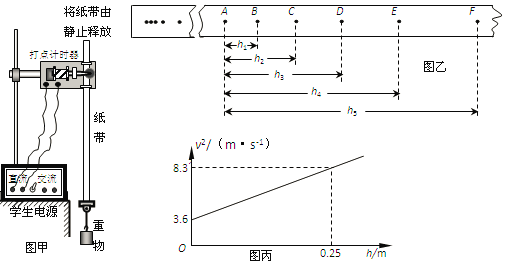
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�����Ŀ��ij��ȤС����ͨ�������б�����˶���ʵ��̽���������������������ٶȱ仯�Ĺ�ϵ����ʵ�鿪ʼǰ��������������¼��ֲ��룺��W�� ![]() ����W��v����W��v2 �� ���ǵ�ʵ��װ����ͼ����ʾ��PQΪһ����б���õ�ľ�壬��Q���̶�һ���ٶȴ�������������������ÿ��ͨ��Q��ʱ���ٶȣ���ÿ��ʵ�飬����Ӳ�ͬ��ʼλ�ô��ɾ�ֹ�ͷţ�
����W��v����W��v2 �� ���ǵ�ʵ��װ����ͼ����ʾ��PQΪһ����б���õ�ľ�壬��Q���̶�һ���ٶȴ�������������������ÿ��ͨ��Q��ʱ���ٶȣ���ÿ��ʵ�飬����Ӳ�ͬ��ʼλ�ô��ɾ�ֹ�ͷţ�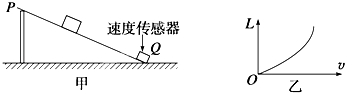
ͬѧ����������±�������¼ʵ�����ݣ�����L1��L2��L3��L4����������ֱ�Ӳ�ͬ��ʼλ�ô������ͷ�ʱ��ʼλ�õ��ٶȴ������ľ��룬v1��v2��v3��v4����ʾ����ÿ��ͨ��Q����ٶȣ�
ʵ����� | 1 | 2 | 3 | 4 | �� |
L | L1 | L1 | L3 | L4 | �� |
v | v1 | v2 | v3 | v4 | �� |
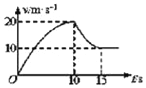
���Ǹ���ʵ�����ݻ�������ͼ����ʾ��L��vͼ���ó�����W��v2 ��
��1������Ϊ���ǵ������Ƿ���ʣ�
��2������ʲô�õĽ��飿
��3���ڴ�ʵ���У�ľ���������Ħ�����Ĵ�С����ᡱ���ᡱ��Ӱ��̽�����Ľ����