题目内容
7.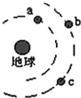 如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗人造地球卫星,a、b质量相同,且小于c的质量,则( )| A. | a 所需向心力最大 | |
| B. | b、c周期相等,且小于a的周期 | |
| C. | b、c的线速度大小相等,且小于a的线速度 | |
| D. | b、c的向心加速度大小相等,且大于a的向心加速度 |
分析 根据人造卫星的万有引力等于向心力,列式求出线速度、角速度、周期和向心力的表达式进行讨论即可.
解答 解:人造卫星绕地球做匀速圆周运动,万有引力提供向心力,设卫星的质量为m、轨道半径为r、地球质量为M,
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r=ma=m$\frac{{v}^{2}}{r}$
A、F=$\frac{GMm}{{r}^{2}}$,因为ra<rb=rc,ma=mb<mc,所以b所需向心力最小,故A错误;
B、T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,因为ra<rb=rc,所以Ta<Tb=Tc,故B正确;
C、v=$\sqrt{\frac{GM}{r}}$,因为ra<rb=rc,所以va>vb=vc,故C正确;
D、a=$\frac{GM}{{r}^{2}}$,因为ra<rb=rc,所以aa>ab=ac,故D错误;
故选:BC.
点评 本题关键抓住万有引力提供向心力,先列式求解出线速度、角速度、周期和加速度的表达式,再进行讨论.

练习册系列答案
相关题目
19.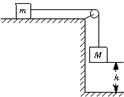 如图所示,质量为m的木块放在光滑的水平桌面上,用轻绳绕过桌边的定滑轮与质量为M的砝码相连,已知M=2m,让绳拉直后使砝码从静止开始下降h(小于桌面)的距离,木块仍没离开桌面,则砝码的速率为( )
如图所示,质量为m的木块放在光滑的水平桌面上,用轻绳绕过桌边的定滑轮与质量为M的砝码相连,已知M=2m,让绳拉直后使砝码从静止开始下降h(小于桌面)的距离,木块仍没离开桌面,则砝码的速率为( )
 如图所示,质量为m的木块放在光滑的水平桌面上,用轻绳绕过桌边的定滑轮与质量为M的砝码相连,已知M=2m,让绳拉直后使砝码从静止开始下降h(小于桌面)的距离,木块仍没离开桌面,则砝码的速率为( )
如图所示,质量为m的木块放在光滑的水平桌面上,用轻绳绕过桌边的定滑轮与质量为M的砝码相连,已知M=2m,让绳拉直后使砝码从静止开始下降h(小于桌面)的距离,木块仍没离开桌面,则砝码的速率为( )| A. | $\frac{1}{3}\sqrt{6gh}$ | B. | $\sqrt{mgh}$ | C. | $\sqrt{2gh}$ | D. | $\frac{2}{3}\sqrt{3gh}$ |
18.(多选)如图所示,小球m在竖直放置的光滑的圆形管道内做圆周运动,下列说法正确的是( )
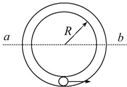

| A. | 小球通过最高点时的最小速度是$\sqrt{gR}$ | |
| B. | 小球通过最高点时的最小速度为零 | |
| C. | 小球通过最低点时对管壁压力一定大于重力 | |
| D. | 小球在水平线ab以下的管道中运动时外侧管壁对小球一定有作用力 |
15.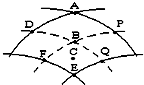 如图所示表示两列相干水波的叠加情况,图中的实线表示波峰,虚线表示波谷.设两列波的振幅均为5cm,且图示的范围内振幅不变,波速和波长分别均为1m/s和0.5m.C点是BE连线的中点,下列说法中不正确的是( )
如图所示表示两列相干水波的叠加情况,图中的实线表示波峰,虚线表示波谷.设两列波的振幅均为5cm,且图示的范围内振幅不变,波速和波长分别均为1m/s和0.5m.C点是BE连线的中点,下列说法中不正确的是( )
 如图所示表示两列相干水波的叠加情况,图中的实线表示波峰,虚线表示波谷.设两列波的振幅均为5cm,且图示的范围内振幅不变,波速和波长分别均为1m/s和0.5m.C点是BE连线的中点,下列说法中不正确的是( )
如图所示表示两列相干水波的叠加情况,图中的实线表示波峰,虚线表示波谷.设两列波的振幅均为5cm,且图示的范围内振幅不变,波速和波长分别均为1m/s和0.5m.C点是BE连线的中点,下列说法中不正确的是( )| A. | C点始终保持静止不动 | |
| B. | 图示时刻A、B两点的竖直高度差为20cm | |
| C. | 图示时刻C点正处于平衡位置且向水面上运动 | |
| D. | 从图示的时刻起经0.25s,B点通过的路程为20cm |
2.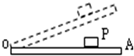 如图所示,重物P放在一长木板OA上,在将长木板绕O端转过一个小角度的过程中,重物P相对于木板始终保持静止.关于木板对重物P的摩擦力和弹力的做功情况是( )
如图所示,重物P放在一长木板OA上,在将长木板绕O端转过一个小角度的过程中,重物P相对于木板始终保持静止.关于木板对重物P的摩擦力和弹力的做功情况是( )
 如图所示,重物P放在一长木板OA上,在将长木板绕O端转过一个小角度的过程中,重物P相对于木板始终保持静止.关于木板对重物P的摩擦力和弹力的做功情况是( )
如图所示,重物P放在一长木板OA上,在将长木板绕O端转过一个小角度的过程中,重物P相对于木板始终保持静止.关于木板对重物P的摩擦力和弹力的做功情况是( )| A. | 摩擦力对重物不做功 | B. | 摩擦力对重物做负功 | ||
| C. | 弹力对重物不做功 | D. | 弹力对重物做负功 |
12.下列关于平抛运动的说法正确的是( )
| A. | 平抛运动是匀速运动 | |
| B. | 平抛运动在相同的时间内速度变化不同 | |
| C. | 平抛运动是匀变速曲线运动 | |
| D. | 以上说法均不正确 |
19.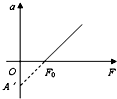 地面上有一重物,用力F向上提它,力F的变化将引起物体加速度的变化.已知物体的加速度a随力F变化的函数图象如图所示,以下说法中错误的是( )
地面上有一重物,用力F向上提它,力F的变化将引起物体加速度的变化.已知物体的加速度a随力F变化的函数图象如图所示,以下说法中错误的是( )
 地面上有一重物,用力F向上提它,力F的变化将引起物体加速度的变化.已知物体的加速度a随力F变化的函数图象如图所示,以下说法中错误的是( )
地面上有一重物,用力F向上提它,力F的变化将引起物体加速度的变化.已知物体的加速度a随力F变化的函数图象如图所示,以下说法中错误的是( )| A. | 当F小于F0时,物体的重力大于作用力F | |
| B. | 重物的质量为m=-$\frac{{F}_{0}}{A′}$ | |
| C. | 物体向上运动的加速度与作用力F成正比 | |
| D. | A′的绝对值等于该地的重力加速度g的大小 |
17.下列关于简谐运动的振幅、周期和频率的说法正确的是( )
| A. | 振幅是矢量,方向从平衡位置指向最大位移处 | |
| B. | 周期和频率的乘积不一定等于1 | |
| C. | 振幅增加,周期必然增加,而频率减小 | |
| D. | 做简谐运动的物体,其频率固定,与振幅无关 |