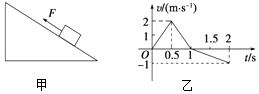题目内容
【题目】某物理课外小组利用图（a）中的装置探究物体加速度与其所受合外力之间的关系．图中，置于实验台上的长木板水平放置，其右端固定一轻滑轮；轻绳跨过滑轮，一端与放在木板上的小滑车相连，另一端可悬挂钩码．本实验中可用的钩码共有N=5个，每个质量均为0.010kg．实验步骤如下：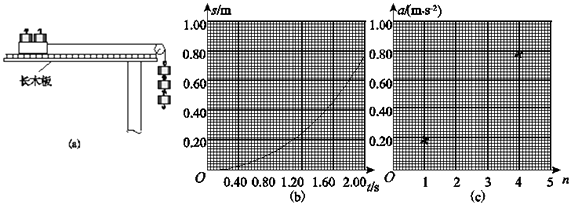
⑴将5个钩码全部放入小车中，在长木板左下方垫上适当厚度的小物块，使小车（和钩码）可以在木板上匀速下滑．
⑵将n（依次取n=1，2，3，4，5）个钩码挂在轻绳右端，其余N﹣n个钩码仍留在小车内；用手按住小车并使轻绳与木板平行．释放小车，同时用传感器记录小车在时刻t相对于其起始位置的位移s，绘制s﹣t图象，经数据处理后可得到相应的加速度a．
⑶对应于不同的n的a值见表．n=2时的s﹣t图象如图（b）所示：由图（b）求出此时小车的加速度（保留2位有效数字），将结果填入表．
n | 1 | 2 | 3 | 4 | 5 |
a（m/s2） | 0.20 | 0.58 | 0.78 | 1.00 |
⑷利用表中的数据在图（c）中补齐数据点，并作出a﹣n图象 ． 从图象可以看出：当物体质量一定时，物体的加速度与其所受的合外力成正比．
⑸利用a﹣n图象求得小车（空载）的质量为kg（保留2位有效数字，g=9.8m/s2）．
⑹若以“保持木板水平”来代替步骤（1），下列说法正确的是（填入正确选项前的标号）
A．a﹣n图线不再是直线
B．a﹣n图线仍是直线，但该直线不过原点
C．a﹣n图线仍是直线，但该直线的斜率变大．
【答案】0.40；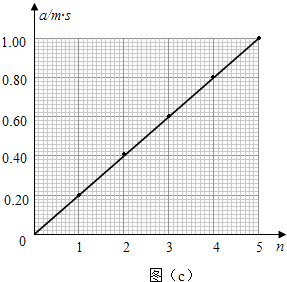
；0.45；BC
【解析】（3）物体做匀加速直线运动，对应的x﹣t图象为曲线，由图象可知，当t=2.0s时，位移为：x=0.80m；
则由x= 
at2代入数据得：a=0.40m/s2；（5）由图c可知，当n=4时，加速度为0.78m/s2，由牛顿第二定律可知：
4×0.01×9.8=（m+5×0.01）×0.78
解得：m=0.45kg；（6）若木板水平，则物体将受到木板的摩擦力；则有：
nm0g﹣μ[m+（5﹣n）m0g]=（m+5m0）a；
a= 
﹣ 
= 
n﹣ 
故说明图象仍为直线，但不再过原点；并且斜率增大；故A错误，BC正确；
（3）根据x﹣t图象的性质可明确各时刻对应的位移，根据位移公式可求得加速度；（4）将点（2，0.40）作出，并用直线将各点连接即可得出图象；（5）找出图象上的点，根据图象的性质以及牛顿第二定律列式，即可求出小车的质量；（6）对实验原理进行分析，明确摩擦力带来的影响；根据牛顿第二定律可明确图象的变化情况．
故答案为：（3）0.40； （4）如上图所示；（5）0.45；（6）BC．
