Question

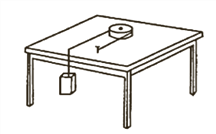
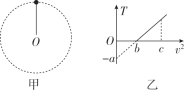
【题目】如图甲所示，用一轻质绳拴着一质量为m的小球，在竖直平面内做圆周运动(不计一切阻力)，小球运动到最高点时绳对小球的拉力为T，小球在最高点的速度大小为v，其T—v2图象如图乙所示，则（ ）

A.轻质绳长为

B.当地的重力加速度为

C.当v2＝c时，轻质绳的拉力大小为

D.只要v2≥b，小球在最低点和最高点时绳的拉力差均为5a

Answer 1

【答案】C

【解析】

AB．在最高点，根据

得

可知纵轴截距的绝对值为

解得当地的重力加速度

图线的斜率

解得绳子的长度

故AB错误；

C．当v2=c时，轻质绳的拉力大小为

故C正确；

D．当v2=b时，轻质绳的拉力大小为T=0，重力提供向心力

当小球运动到最低点时速度为v′，根据动能定理可知

最低点，根据向心力公式可知

联立解得

故D错误。

故选C。