题目内容
12. 如图所示,一矩形线圈在匀强磁场中绕OO′轴匀速转动,磁场方向与转轴垂直.已知线圈匝数n=200,电阻r=1Ω,长L1=0.1m,宽L2=0.04m,角速度=l00rad/s,磁场的磁感应强度B=0.25T.线圈两端外接电阻R=4Ω的用电器和一个交流电流表(内阻不计),求:
如图所示,一矩形线圈在匀强磁场中绕OO′轴匀速转动,磁场方向与转轴垂直.已知线圈匝数n=200,电阻r=1Ω,长L1=0.1m,宽L2=0.04m,角速度=l00rad/s,磁场的磁感应强度B=0.25T.线圈两端外接电阻R=4Ω的用电器和一个交流电流表(内阻不计),求:(1)电流表
 的读数.
的读数.(2)用电器上消耗的电功率.
(3)从图示位置转过60°过程中经过
 表的电量.
表的电量.
分析 (1)线圈中产生的感应电动势的最大值表达式为Em=NBSω.电流表测量电流的有效值.根据E=$\frac{{E}_{m}}{\sqrt{2}}$和欧姆定律求出电流的有效值.
(2)用电器消耗的电功率P=I2R,I是电流的有效值.
(3)$\overline{E}$=n$\frac{△φ}{△t}$计算平均感应电动势,由q=It可求得电量.
解答 解:(1)线圈中产生的感应电动势的最大值表达式为:Em=nBSω
代入数据得:Em=200×0.25×0.1×0.04×l00 V=20 V
根据欧姆定律得:Im=$\frac{{E}_{m}}{R+r}$
代入数据得:Im=$\frac{20}{5+1}$A=$\frac{10}{3}$A
因为是正弦交变电流,所以电流表读数即有效值:
I=$\frac{{I}_{m}}{\sqrt{2}}$A=$\frac{10}{3×\sqrt{2}}$=2.34A
(2)用电器所消耗的电功率:P=I2R=2.342×5W=27.38W.
(4)转过60°的过程,需要时间:t=$\frac{2π}{100}×\frac{1}{6}$=$\frac{π}{300}$s
根据法拉第电磁感应定律:$\overline{E}$=n$\frac{△φ}{△t}$=200×$\frac{BS-BScos60°}{t}$
电量Q=It=$\frac{\overline{E}}{R+r}△t$=$\frac{nBS}{R+r}$=$\frac{200×\frac{1}{2}×0.25×0.1×0.04}{5+1}$=0.02C;
答:(1)电流表A的读数2.34A.
(3)用电器上消耗的电功率27.38W.
(4)电量为0.02C.
点评 本题考查交变电流最大值、有效值的理解和应用的能力,对于交流电表的测量值、计算交流电功率、电功等都用到有效值.

| A. | $\frac{1}{50}$s | B. | $\frac{1}{100}$s | C. | $\frac{1}{150}$s | D. | $\frac{1}{200}$s |
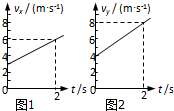 某质点在xOy平面内运动,从t=0时刻起,它在x轴方向和y轴方向的v-t图象分别如图1和图2所示,则下列判断正确的是( )
某质点在xOy平面内运动,从t=0时刻起,它在x轴方向和y轴方向的v-t图象分别如图1和图2所示,则下列判断正确的是( )| A. | 该质点可能做匀变速曲线运动 | B. | 该质点一定做匀加速直线运动 | ||
| C. | 该质点的初速度大小为7m/s | D. | 该质点的加速度大小为2.5m/s2 |
 波源S在t=0时刻从平衡位置开始向上运动,形成向左右两侧传播的简谐横波.S、a、b、c、d、e和a′、b′、c′是沿波传播方向上的间距为lm的9个质点,t=0时刻均静止于平衡位置,如图所示.当t=0.1s时质点S第一次到达最高点,当t=0.4s时质点d开始起振.则以下说法正确的是( )
波源S在t=0时刻从平衡位置开始向上运动,形成向左右两侧传播的简谐横波.S、a、b、c、d、e和a′、b′、c′是沿波传播方向上的间距为lm的9个质点,t=0时刻均静止于平衡位置,如图所示.当t=0.1s时质点S第一次到达最高点,当t=0.4s时质点d开始起振.则以下说法正确的是( )| A. | 该波的波速为10m/s | |
| B. | t=0.4s这一时刻质点a的速度最大 | |
| C. | t=0.4s这一时刻质点c的加速度最大 | |
| D. | t=0.5s这一时刻质点c′已经振动了0.2s |
 如图所示,倒悬的导热气缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定质量的理想气体.起初各部分均静止不动,大气压强保持不变.对于汽缸内的气体,当其状态缓慢发生变化时,下列判断正确的是( )
如图所示,倒悬的导热气缸中有一个可无摩擦上下移动且不漏气的活塞A,活塞A的下面吊着一个重物,汽缸中封闭着一定质量的理想气体.起初各部分均静止不动,大气压强保持不变.对于汽缸内的气体,当其状态缓慢发生变化时,下列判断正确的是( )| A. | 若环境温度升高,则气体的压强一定增大 | |
| B. | 当活塞向下移动时,外界对气体做功 | |
| C. | 保持环境温度不变,缓慢增加重物的质量,气体一定会吸热 | |
| D. | 若环境温度降低,缓慢增加重物的质量,气体体积可能保持不变 |
 位于竖直平面内矩形平面导线框abcd.水平边ab长L1=1.0m,竖直边ad长L2=0.5m,线框的质量m=0.2kg,线框的电阻R=2Ω,其下方有一匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行.两边界间距离为H,H>L2,磁场的磁感应强度B=1.0T,方向与线框平面垂直.如图所示,令线框的dc边从离磁场区域上边界PP′的距离为h=0.7m处自由下落.已知线框dc进入磁场以后,ab边到达边界PP′之前的某一时刻线框的速度已到达这一段的最大值.问从线框开始下落到dc边刚刚到达磁场区域下边界QQ′过程中,线框克服安培力做的总功为多少?(取g=10m/s2,不计空气阻力)
位于竖直平面内矩形平面导线框abcd.水平边ab长L1=1.0m,竖直边ad长L2=0.5m,线框的质量m=0.2kg,线框的电阻R=2Ω,其下方有一匀强磁场区域,该区域的上、下边界PP′和QQ′均与ab平行.两边界间距离为H,H>L2,磁场的磁感应强度B=1.0T,方向与线框平面垂直.如图所示,令线框的dc边从离磁场区域上边界PP′的距离为h=0.7m处自由下落.已知线框dc进入磁场以后,ab边到达边界PP′之前的某一时刻线框的速度已到达这一段的最大值.问从线框开始下落到dc边刚刚到达磁场区域下边界QQ′过程中,线框克服安培力做的总功为多少?(取g=10m/s2,不计空气阻力) 如图所示,某学校趣味运动会上举行推箱子比赛.杨明同学用与水平方向成θ=30°角斜向下的推力F推一个重为G=200N的箱子匀速前进,箱子与地面间的动摩擦因数为μ=0.40.求:
如图所示,某学校趣味运动会上举行推箱子比赛.杨明同学用与水平方向成θ=30°角斜向下的推力F推一个重为G=200N的箱子匀速前进,箱子与地面间的动摩擦因数为μ=0.40.求: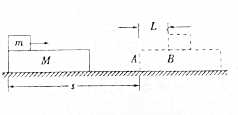 质量为M的长木板放在光滑的水平面上(如图所示).一个质量为m的滑块以某一速度沿木板上表面从A点滑至B点,在木板上前进了s,若滑块与木板间的动摩擦因数为μ,求:
质量为M的长木板放在光滑的水平面上(如图所示).一个质量为m的滑块以某一速度沿木板上表面从A点滑至B点,在木板上前进了s,若滑块与木板间的动摩擦因数为μ,求: 质量都是1kg的物体A,B中间用一轻弹簧连接,放在光滑的水平地面上,现使B物体靠在墙上,用力推物体A压缩弹簧,如图所示,这个过程中外力做功为8J,待系统静止后突然撤去外力,从撤去外力到弹簧第一次恢复到原长时B物体的动量为0,当A,B间距离最大时B物体的速度大小为2m/s.
质量都是1kg的物体A,B中间用一轻弹簧连接,放在光滑的水平地面上,现使B物体靠在墙上,用力推物体A压缩弹簧,如图所示,这个过程中外力做功为8J,待系统静止后突然撤去外力,从撤去外力到弹簧第一次恢复到原长时B物体的动量为0,当A,B间距离最大时B物体的速度大小为2m/s.