题目内容
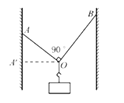
【题目】在如图所示，AB 为粗糙绝缘水平桌面,BQ 为竖直平面内半径为 R=0.5m 的四分之一光滑绝缘圆弧轨道，固定在 AB 右端,与 AB 平滑连接。在水平桌面上距 B 端 s=1m 处放一质量
为 m=1kg 的带正电的小物块（可视为质点），电量为小物块与桌面之间的动摩擦因数为 μ=0.25。现在在竖直线 OB 左侧空间加一电场强度 E=105 N/C、方向与水平方向成37°斜向下的匀强电场，同时在小物块上施加 F=6N 的水平向左的恒力。（重力加速度 g=10m/s2，sin370=0.6，cos370 = 0.8，设小物块与桌面间的最大静摩擦力等于滑动摩擦力）。
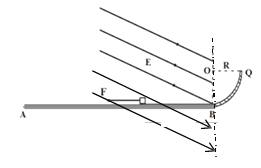
（1）求小物块所受的摩擦力大小；
（2）若撤去拉力 F，求小物块第一次到达 B 点时的速度大小；
（3）若撤去拉力 F，求小物块在水平桌面上的运动总路程。
【答案】（1）
（2）
（3）
【解析】
（1）将电场力分解成水平方向与竖直方向，再根据滑动摩擦力，来确定最大静摩擦力，从而确定小物块是否运动，进而确定摩擦力大小；（2）撤去F后，确定小物块的合力，再根据动能定理，即可求解小物块第一次到达 B 点时的速度大小；（3）撤去F后，整个过程运用动能定理即可求出小物块在水平桌面上的运动总路程。
（1）电场力在水平方向的分力为：
，
电场力在竖直方向的分力为：
小物块与木板间的最大静摩擦力为：
由于
，所以小物块保持静止
所以小物块受静摩擦力为：
（2）撤去F后，小物块向右加速，木板仍然静止
小物块受合力为：
小物块从开始至运动到B点，由动能定理得：
B点速度为：
（3）撤去F后，最后小物块停在水平桌面上，整个过程运用动能定理得：
解得：
练习册系列答案
优加精卷系列答案
相关题目
