题目内容
在高速公路的拐弯处，路面造得外高内低，即当车向右拐弯时，司机左侧的路面比右侧的要高一些，路面与水平面间的夹角为θ，设拐弯路段是半径为R的圆弧，要使车速为v时车轮与路面之间的横向（即垂直于前进方向）摩擦力等于零，则tanθ=
．
| v2 |
| Rg |
| v2 |
| Rg |
分析：车做匀速圆周运动，重力和支持力的合力巧好提供向心力，根据牛顿第二定律列式求解即可．
解答：解：车匀速转弯，合力等于向心力，如图
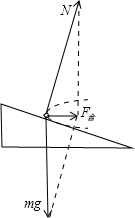
根据牛顿第二定律
mgtanθ=m
解得
tanθ=
故答案为：
根据牛顿第二定律
mgtanθ=m
| v2 |
| R |
解得
tanθ=
| v2 |
| Rg |
故答案为：
| v2 |
| Rg |
点评：本题关键找到向心力来源，然后根据牛顿第二定律列式求解．
练习册系列答案
阅读快车系列答案
相关题目
在高速公路的拐弯处，路面造得外高内低，即当车向右拐弯时，司机左侧的路面比右侧的要高一些，路面与水平面间的夹角为θ设拐弯路段是半径为R的圆弧，要使车速为v时车轮与路面之间的横向（即垂直于前进方向）摩擦力等于零，θ应满足（ ）