题目内容
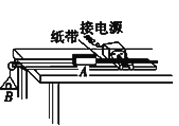
【题目】如图1，光滑绝缘水平平台MNQP为矩形，GH∥PQ，MP=NQ=1m，MN=GH=PQ=0.4m，平台离地面高度为h=2.45m。半径为R=0.2m的圆形匀强磁场区域，磁感应强度B=0.05T，方向竖直向上，与MP边相切于A点，与NQ边相切于D点，与GH相切于C点。平台上PGHQ区域内有方向由P指向G的匀强电场，场强大小为E=0.25V/m。平台右方整个空间存在方向水平向右的电场，场强大小也为E=0.25V/m，俯视图如图2。两个质量均为m=2×10-5kg的小球a、b，小球a带正电，电量q=4×10-4C，小球b不带电，小球a、b均可视为质点。小球a从A点正对圆心O射入磁场，偏转90°后离开磁场，一段时间后与静止在平台D点的小球b发生弹性碰撞，碰后两球离开平台，并在此后的运动过程中发生多次弹性碰撞，a球带电量始终不变，碰撞时间忽略不计。已知重力加速度g=10m/s2，π=3.14，不计空气阻力，求：
(1)小球a射入磁场时的速度大小；
(2)从小球a射入磁场到第一次与小球b相碰撞，小球a运动的路程；
(3)两个小球落地点与NQ的水平距离。
【答案】（1）0.2m/s （2）0.636m（3）0.684m
【解析】
(1)小球a从A点正对圆心O射入磁场，偏转90°后离开磁场，小球a在洛伦兹力作用下做圆周运动，轨迹如图：
分析得半径R=0.2m
由
得：v=0.2m/s
(2)磁场中运动的路程s1=πR=0.628m
电场中加速度
电场的路程
小球a射入磁场到与小球b相碰过程运动的路程
(3)a、b球弹性碰撞，质量相等每一次碰撞速度交换。
D点碰后，两球速度分别为vaD=0，vbD=0.2m/s
此后两球抛离平台，竖直方向均做自由落体运动
由
得，两小球在空中运动时间
水平方向：b球匀速运动，a球加速运动，加速度
每次碰到下一次碰撞，两球位移相等，v—t图如图所示：
可得，每两次碰撞间隔时间是定值：
由
所以小球在空中碰8次后，再过0.06s落地
小球b在空中碰n次后速度为vbN=(n+1)vbD=0.2(n+1) m/s
小球离开D点后在空中第一次碰撞前，水平位移x1=vb1·△t=0.016m
小球在空中第一次到第二次碰撞水平位移x2=2vb1·△t=0.032m
以此类推，小球在空中第n-1次到第n次碰撞水平位移xn=nx1=0.016m
所以，在空中碰撞8次时的水平位移x0=0.016×（1+2+3+4+5+6+7+8）=0.576m
第8次碰后
vb8=1.8m/s
va8=1.6m/s
所以，8次碰后0.06s内，△xb=vb8×0.06=0.108m
△xa=va8×0.06+
×0.062=0.105m
所以，水平位移分别为xa=x0+△xa=0.681m
xb=x0+△xb=0.684m
