题目内容
2. 如图所示,一内壁光滑的固定圆锥形漏斗,其中心轴线竖直,有两个质量相同的小球A和B,分别紧贴着漏斗壁在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,则( )
如图所示,一内壁光滑的固定圆锥形漏斗,其中心轴线竖直,有两个质量相同的小球A和B,分别紧贴着漏斗壁在水平面内做匀速圆周运动,其中小球A的位置在小球B的上方,则( )| A. | A球的速率小于B球的速率 | |
| B. | A球的角速度大于B球的角速度 | |
| C. | A球的转动周期大于B球的转动周期 | |
| D. | A球对漏斗壁的压力大于B球对漏斗壁的压力 |
分析 小球受重力和支持力,靠重力和支持力的合力提供圆周运动的向心力,根据牛顿第二定律得出线速度、角速度和支持力的表达式,从而分析判断.
解答 解:AB、对小球受力分析,小球受到重力和支持力,它们的合力提供向心力,如图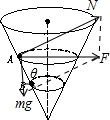
根据牛顿第二定律,有:
F=mgtanθ=$m\frac{{v}^{2}}{r}=mr{ω}^{2}$,解得$v=\sqrt{grtanθ}$,$ω=\sqrt{\frac{gtanθ}{r}}$,A的转动半径大,则A的线速度较大,角速度较小,故A、B错误.
C、因为A的角速度小于B的角速度,根据T=$\frac{2π}{ω}$知,A的转动周期大于B球的转动周期,故C正确.
D、因为支持力N=$\frac{mg}{cosθ}$,支持力等于球对筒壁的压力,知球A对筒壁的压力一定等于球B对筒壁的压力.故D错误.
故选:C.
点评 解决本题的关键知道圆周运动向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
12.一颗小行星绕太阳做匀速圆周运动的半径是地球公转半径的4倍,则这颗小行星运转的周期是( )
| A. | 4年 | B. | 6年 | C. | 8年 | D. | $\frac{8}{9}$年 |
10.分别用红光和绿光在同一双缝干涉实验装置做实验,下列说法正确的是( )
| A. | 红光频率小,条纹间距小 | B. | 红光频率小,条纹间距大 | ||
| C. | 绿光波长大,条纹间距小 | D. | 绿光波长大,条纹间距大 |
17.一个物体做曲线运动,则这个物体( )
| A. | 一定是做加速度不变的运动 | |
| B. | 一定是做加速度变化的运动 | |
| C. | 做速度大小不断变化但速度方向可能不变的运动 | |
| D. | 做速度方向不断变化但速度大小可能不变的运动 |
7. 如图所示,一根轻弹簧下端固定,竖直静止在水平面上,其正上方A位置处有一个小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在下落阶段( )
如图所示,一根轻弹簧下端固定,竖直静止在水平面上,其正上方A位置处有一个小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在下落阶段( )
 如图所示,一根轻弹簧下端固定,竖直静止在水平面上,其正上方A位置处有一个小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在下落阶段( )
如图所示,一根轻弹簧下端固定,竖直静止在水平面上,其正上方A位置处有一个小球.小球从静止开始下落,在B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.在下落阶段( )| A. | 小球在B位置动能最大 | |
| B. | 小球在C位置动能最大 | |
| C. | 从A→C的过程中,小球重力势能的减少量等于动能的增加量 | |
| D. | 从A→D的过程中,小球重力势能的减小量等于弹簧弹性势能的增加量 |
14. 如图所示,有一个半径为R的光滑圆形圆管轨道(忽略圆管内径),一小球处于圆管内,现给小球有一个初速度,使小球在竖直面内做圆周运动,小球过最高点的速度为v,下列叙述正确的是( )
如图所示,有一个半径为R的光滑圆形圆管轨道(忽略圆管内径),一小球处于圆管内,现给小球有一个初速度,使小球在竖直面内做圆周运动,小球过最高点的速度为v,下列叙述正确的是( )
 如图所示,有一个半径为R的光滑圆形圆管轨道(忽略圆管内径),一小球处于圆管内,现给小球有一个初速度,使小球在竖直面内做圆周运动,小球过最高点的速度为v,下列叙述正确的是( )
如图所示,有一个半径为R的光滑圆形圆管轨道(忽略圆管内径),一小球处于圆管内,现给小球有一个初速度,使小球在竖直面内做圆周运动,小球过最高点的速度为v,下列叙述正确的是( )| A. | 小球过最低点的最小速度为2$\sqrt{gR}$ | |
| B. | v增大,轨道对球的弹力也增大 | |
| C. | 当v由$\sqrt{gR}$值逐渐减小时,轨道对小球的弹力也逐渐减小 | |
| D. | 当v由$\sqrt{gR}$值逐渐增大时,轨道对小球的弹力也逐渐增大 |
11.一正弦交流电的电压随时间变化的规律如图所示.由图可知( )


| A. | 该交流电的电压瞬时值的表达式为μ=100sin(25πt)V | |
| B. | 该交流电的频率为50Hz | |
| C. | 该交流电的电压的有效值为100$\sqrt{2}$ | |
| D. | 若将该交流电压加在阻值R=100Ω的电阻两端,则电阻消耗的功率是50W |
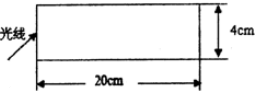 如图所示,用折射率为$\frac{2}{\sqrt{3}}$的透明材料制成的圆柱形棒,其直径为4cm,长为20cm.一束光线射向圆柱棒一个底面的中心,折射入圆柱棒后再由棒的另一底面射出,该光线经历的全反射次数最多为( )
如图所示,用折射率为$\frac{2}{\sqrt{3}}$的透明材料制成的圆柱形棒,其直径为4cm,长为20cm.一束光线射向圆柱棒一个底面的中心,折射入圆柱棒后再由棒的另一底面射出,该光线经历的全反射次数最多为( )