题目内容
18. 如图所示,两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A,B运动的线速度大小分别为v1和v2,星球B与O点之间的距离为L,已知A,B的中心和O三点始终共线,A和B分别在O的两侧,引力常数为G,求:
如图所示,两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A,B运动的线速度大小分别为v1和v2,星球B与O点之间的距离为L,已知A,B的中心和O三点始终共线,A和B分别在O的两侧,引力常数为G,求:(1)两星球做圆周运动的周期
(2)星球A,B的总质量.
分析 该题属于双星问题,它们之间的万有引力提供向心力,它们两颗星的轨道半径的和等于它们之间的距离.代入公式即可解答
解答 解:(1)A和B和O始终共线,说明A和B有相同的角速度和周期,根据周期和线速度的关系得:$T=\frac{2πL}{{v}_{2}}$,
(2)设A到O的距离为R,根据v1=ωR,v2=ωL,解得:$R=\frac{{v}_{1}}{{v}_{2}}L$
根据万有引力提供向心力得:
对A星球,$G\frac{{m}_{A}{m}_{B}}{(R+L)^{2}}={m}_{A}\frac{{{v}_{1}}^{2}}{R}$,
对B星球,$G\frac{{m}_{A}{m}_{B}}{{(R+L)}^{2}}={m}_{B}\frac{{{v}_{2}}^{2}}{L}$
解得:mA+mB=$\frac{{v}_{1}{v}_{2}(\frac{{v}_{1}}{{v}_{2}}+1)^{2}L+{{v}_{2}}^{2}(\frac{{v}_{1}}{{v}_{2}}+1)^{2}L}{G}$
答:(1)两星球做圆周运动的周期为$\frac{2πL}{{v}_{2}}$;
(2)星球A,B的总质量为$\frac{{v}_{1}{v}_{2}{(\frac{{v}_{1}}{{v}_{2}}+1)}^{2}L+{{v}_{2}}^{2}{(\frac{{v}_{1}}{{v}_{2}}+1)}^{2}L}{G}$.
点评 该题属于双星问题,有两星球之间的万有引力提供向心力,知道两颗星的轨道半径的和等于它们之间的距离,不能把它们的距离当成轨道半径.

练习册系列答案
相关题目
9. 2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则( )
2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则( )
 2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则( )
2010年10月1日18时59分57秒,搭载着嫦娥二号卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,卫星由地面发射后,进入地月转移轨道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道,开始对月球进行探测,则( )| A. | 卫星在轨道Ⅲ上的运动速度比月球的第一宇宙速度小 | |
| B. | 卫星在轨道Ⅲ上经过P点的速度比在轨道Ⅰ上经过P点时大 | |
| C. | 卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上短 | |
| D. | 卫星在轨道Ⅰ上经过P点比在轨道Ⅱ上经过P点时的速度大 |
19. 如图中带箭头的实线表示某个电场的电场线,实线间距相等且相互平行,一个带电离子从P处飞入这个电场(如图所示),以下说法中正确的是( )
如图中带箭头的实线表示某个电场的电场线,实线间距相等且相互平行,一个带电离子从P处飞入这个电场(如图所示),以下说法中正确的是( )
 如图中带箭头的实线表示某个电场的电场线,实线间距相等且相互平行,一个带电离子从P处飞入这个电场(如图所示),以下说法中正确的是( )
如图中带箭头的实线表示某个电场的电场线,实线间距相等且相互平行,一个带电离子从P处飞入这个电场(如图所示),以下说法中正确的是( )| A. | 离子受的电场力方向一定向右 | B. | 离子受的电场力大小、方向都不变 | ||
| C. | 离子电势能肯定减少 | D. | 离子一定做匀变速运动 |
20.关于布朗运动,下列说法中正确的是( )
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 温度降到0℃时,布朗运动会停止 | |
| C. | 时间足够长,布朗运动将会逐渐变慢而停止 | |
| D. | 布朗运动产生的原因不在外界而在液体内部 |
 如图,电源电动势E=12V,内阻r=1Ω,电阻R1=4Ω,R2=22Ω,滑动变阻器R的阻值0~30Ω.闭合电键S,当滑动变阻器的滑动触头P由a端向b端滑动时,理想电流表和理想电压表示数变化量的大小分别用△I、△U表示.则$\frac{△U}{△I}$5Ω;R1消耗的最小电功率为P=1.78W.
如图,电源电动势E=12V,内阻r=1Ω,电阻R1=4Ω,R2=22Ω,滑动变阻器R的阻值0~30Ω.闭合电键S,当滑动变阻器的滑动触头P由a端向b端滑动时,理想电流表和理想电压表示数变化量的大小分别用△I、△U表示.则$\frac{△U}{△I}$5Ω;R1消耗的最小电功率为P=1.78W.



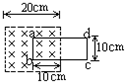 单匝矩形线圈abcd部分地放置在具有理想边界的匀强磁场中,磁感应强度为0.1T,线圈绕ab轴以100p rad/s角速度匀速旋转,如图所示,当线圈由图示位置转过60°,在这过程中感应电动势平均值为多大?当转过90°时,感应电动势即时值为多大?
单匝矩形线圈abcd部分地放置在具有理想边界的匀强磁场中,磁感应强度为0.1T,线圈绕ab轴以100p rad/s角速度匀速旋转,如图所示,当线圈由图示位置转过60°,在这过程中感应电动势平均值为多大?当转过90°时,感应电动势即时值为多大? 如图所示,某人乘雪橇从雪坡经A点滑到B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.开始时人与雪橇距水平路面的高度h=20m,经A、B两点时的速度分别是2m/s和12m/s,g取10m/s2,试求:
如图所示,某人乘雪橇从雪坡经A点滑到B点,接着沿水平路面滑至C点停止.人与雪橇的总质量为70kg.开始时人与雪橇距水平路面的高度h=20m,经A、B两点时的速度分别是2m/s和12m/s,g取10m/s2,试求: 如图所示,圆形区域存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场,一个电荷量为q,质量为m的粒子沿平行于直径AC的方向射入磁场,射入点到直径AC的距离为磁场区域半径的一半,粒子从D点射出磁场时的速率为v,不计粒子的重力.求
如图所示,圆形区域存在磁感应强度大小为B、方向垂直纸面向里的匀强磁场,一个电荷量为q,质量为m的粒子沿平行于直径AC的方向射入磁场,射入点到直径AC的距离为磁场区域半径的一半,粒子从D点射出磁场时的速率为v,不计粒子的重力.求