题目内容
 质量为30kg的小孩坐在10kg的雪橇上,大人用大小为100N、与水平方向成37°斜向上的拉力,从静止开始使雪橇做匀加速直线运动,10s时撤去拉力,使雪橇自由滑行,设雪橇与地面间的动摩擦因数为0.2,(sin37°=0.6,cos37°=0.8,g取10m/s2)求:
质量为30kg的小孩坐在10kg的雪橇上,大人用大小为100N、与水平方向成37°斜向上的拉力,从静止开始使雪橇做匀加速直线运动,10s时撤去拉力,使雪橇自由滑行,设雪橇与地面间的动摩擦因数为0.2,(sin37°=0.6,cos37°=0.8,g取10m/s2)求:(1)10s末雪橇的速度;
(2)雪橇运动的总路程.
分析:(1)对小孩和雪橇整体受力分析,根据牛顿第二定律求得雪橇的加速度,利用速度公式可求速度
(2)雪橇运动的总路程分撤去力F前和撤之后,分别研究受力情况,由牛顿第二定律分别和运动学公式分别求路程,然后加和即雪橇运动的总路程.
(2)雪橇运动的总路程分撤去力F前和撤之后,分别研究受力情况,由牛顿第二定律分别和运动学公式分别求路程,然后加和即雪橇运动的总路程.
解答:解:(1)对小孩和雪橇整体受力分析如图所示:
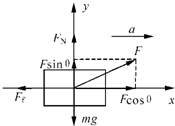
根据牛顿第二定律:
水平方向:Fcosθ-Ff=ma1
竖直方向:FN+Fsinθ-mg=0
又:Ff=μFN
代入数据解得a1=0.3m/s2
根据运动学公式,10s末的速度为v=a1t=3m/s
(2)撤去F前,整体做加速运动,位移x1=
a1
=15m
撤去F后,整体做减速运动,根据牛顿第二定律有:
滑动的加速度为-μmg=ma2
根据运动学公式:0-v2=2ax2
解得:x2=2.25m
雪橇运动的总路程为x=x1+x2=17.25m
答:(1)10s末雪橇的速度为3m/s;
(2)雪橇运动的总路程为17.25m.

根据牛顿第二定律:
水平方向:Fcosθ-Ff=ma1
竖直方向:FN+Fsinθ-mg=0
又:Ff=μFN
代入数据解得a1=0.3m/s2
根据运动学公式,10s末的速度为v=a1t=3m/s
(2)撤去F前,整体做加速运动,位移x1=
| 1 |
| 2 |
| t | 2 |
撤去F后,整体做减速运动,根据牛顿第二定律有:
滑动的加速度为-μmg=ma2
根据运动学公式:0-v2=2ax2
解得:x2=2.25m
雪橇运动的总路程为x=x1+x2=17.25m
答:(1)10s末雪橇的速度为3m/s;
(2)雪橇运动的总路程为17.25m.
点评:解决本题的关键是正确的受力分析,结合牛顿第二定律求得加速度,利用运动学公式求解.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图所示,质量为30kg的小孩坐在质量为10kg的雪橇上,大人用于水平方向成37°斜向上的大小为100N的拉力拉雪橇,使雪橇沿水平地面做匀速直线运动,求:
如图所示,质量为30kg的小孩坐在质量为10kg的雪橇上,大人用于水平方向成37°斜向上的大小为100N的拉力拉雪橇,使雪橇沿水平地面做匀速直线运动,求: 在我国东北寒冷的冬季,狗拉雪橇是人们出行的常见交通工具,如图所示.一质量为30kg的小孩坐在10.6kg的钢制滑板的雪橇上,狗用与水平方向成37°斜向上的拉力拉雪橇,雪橇与冰道间的动摩擦因数为0.02,求狗要用多大的力才能够拉雪橇匀速前进.(sin37°=0.6,cos37°=0.8,g=10m/s2)
在我国东北寒冷的冬季,狗拉雪橇是人们出行的常见交通工具,如图所示.一质量为30kg的小孩坐在10.6kg的钢制滑板的雪橇上,狗用与水平方向成37°斜向上的拉力拉雪橇,雪橇与冰道间的动摩擦因数为0.02,求狗要用多大的力才能够拉雪橇匀速前进.(sin37°=0.6,cos37°=0.8,g=10m/s2) 质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的拉力拉雪橇,力的大小为100N,雪橇与地面间的动摩擦因数为0.2,求:
质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的拉力拉雪橇,力的大小为100N,雪橇与地面间的动摩擦因数为0.2,求: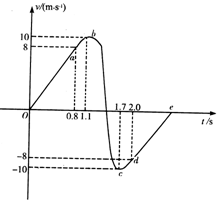 一个质量为30kg的小孩在蹦床上做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他的运动速度随时间变化的图象如图所示,图中只有Oa段和de段为直线.则根据此图象可知,小孩和蹦床相接触的时间内,蹦床对小孩的平均作用力为(空气阻力不计,g取10m/s2)( )
一个质量为30kg的小孩在蹦床上做游戏,他从高处落到蹦床上后又被弹起到原高度,小孩从高处开始下落到弹回的整个过程中,他的运动速度随时间变化的图象如图所示,图中只有Oa段和de段为直线.则根据此图象可知,小孩和蹦床相接触的时间内,蹦床对小孩的平均作用力为(空气阻力不计,g取10m/s2)( )