题目内容
20. 如图,AB为光滑固定的$\frac{1}{4}$圆弧面,其下端B与一木板的上表面光滑连接,木板可以在光滑水平面上自由移动,其左端固定一个轻弹簧,一小物块自A点由静止沿圆弧面下滑,滑上木板后压缩弹簧.若小物块和木板A质量均为m=1kg,圆弧半径R=0.2m,重力加速度g取10m/s2.求当弹簧被压缩到最短时木板的速度和小物块的动能.
如图,AB为光滑固定的$\frac{1}{4}$圆弧面,其下端B与一木板的上表面光滑连接,木板可以在光滑水平面上自由移动,其左端固定一个轻弹簧,一小物块自A点由静止沿圆弧面下滑,滑上木板后压缩弹簧.若小物块和木板A质量均为m=1kg,圆弧半径R=0.2m,重力加速度g取10m/s2.求当弹簧被压缩到最短时木板的速度和小物块的动能.
分析 从A到B由动能定理求得小物块到达B点的速度.小物块在木板上运动的过程,当弹簧被压缩到最短时小物块和木板的速度相同,根据动量守恒定律求出共同速度,再求小物块的动能.
解答 解:小物块从A到B的过程,由动能定理得:
mgR=$\frac{1}{2}m{v}_{B}^{2}$
可得 vB=$\sqrt{2gR}$=$\sqrt{2×10×0.2}$=2m/s
设当弹簧被压缩到最短时木板的速度为v.取水平向左为正方向,根据动量守恒定律得
mvB=2mv
得 v=1m/s
小物块的动能为 Ek=$\frac{1}{2}m{v}^{2}$=$\frac{1}{2}×1×{1}^{2}$=0.5J
答:当弹簧被压缩到最短时木板的速度是1m/s,小物块的动能是0.5J.
点评 分析清楚物体的运动过程,明确物块在木板上运动时系统的动量守恒是关键.要把握每个过程的物理规律,应用动能定理和动量守恒定律解题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
8.以下关于力的说法正确的是( )
| A. | 相互接触的物体间一定存在弹力 | |
| B. | 重力、支持力、压力、摩擦力是根据力的性质来命名的 | |
| C. | 物体处于地球上任一位置的重力方向是相同的,都是竖直向下 | |
| D. | 课本对桌面的压力方向总是垂直接触面指向被压物体 |
8.如图所示的电路中,闭合开关后,将滑动变阻器R的滑片P向上移动,则有( )


| A. | V1表读数变大 | B. | V2表读数变小 | C. | A表读数变小 | D. | 电源的功率变小 |
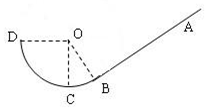 如图所示,粗糙斜面AB与竖直平面内的光滑圆弧轨道BCD相切于B点,圆弧轨道的半径为R,C点在O点正下方,D点与O点在同一水平线上,∠COB=θ.现有一质量为m的物块从D点无初速度释放,物块与斜面间的动摩擦因素为μ,重力加速度为g.求:
如图所示,粗糙斜面AB与竖直平面内的光滑圆弧轨道BCD相切于B点,圆弧轨道的半径为R,C点在O点正下方,D点与O点在同一水平线上,∠COB=θ.现有一质量为m的物块从D点无初速度释放,物块与斜面间的动摩擦因素为μ,重力加速度为g.求: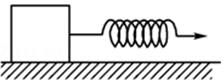 一质量不计的弹簧原长为10cm,一端固定于质量m=2kg的物体上,另一端施一水平拉力F.若物体与水平面间的动摩擦因数为0.2,当弹簧拉长至14cm时,物体恰好被拉动,( g=10m/s2,设最大静摩擦力与滑动摩擦力相等)
一质量不计的弹簧原长为10cm,一端固定于质量m=2kg的物体上,另一端施一水平拉力F.若物体与水平面间的动摩擦因数为0.2,当弹簧拉长至14cm时,物体恰好被拉动,( g=10m/s2,设最大静摩擦力与滑动摩擦力相等)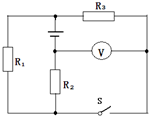 如图所示,R1=R2=R3=10Ω,S断开,电压表示数为8V,S闭合,电压表示数为5V,已知电压表内阻很大.求:
如图所示,R1=R2=R3=10Ω,S断开,电压表示数为8V,S闭合,电压表示数为5V,已知电压表内阻很大.求: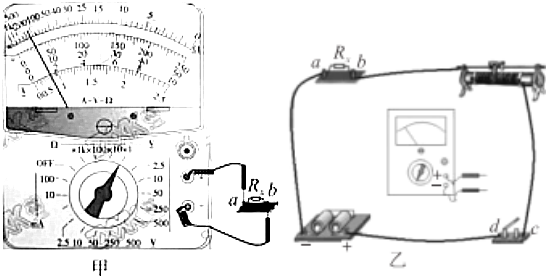
 空气中直径小于等于 2.5 微米的细颗粒物称做PM2.5,其在空气中的含量称作PM值,单位是毫克每立方米.某校“PM2.5兴趣小组”自制了一台静电除尘器,装置呈圆筒形,如图为其截面图.高压电极的负极位于中轴线上,由A、B两段金属构成,A段较粗呈杆状,B段较细呈针状,收尘区由半径为R的圆柱形的金属筒壁构成,接高压电源的正极.圆筒中气体分子中的电子和带正电的部分由于受到方向相反的强大的静电力而电离.一部分细颗粒物吸附了电子而带负电,所有带负电的细颗粒物都飞向筒壁,最后在重力的作用下落在筒底,空气因此而变得清洁.在一次试验中,含尘气体由底部吹入,气流速度恒为v,高压电源的恒定不变,工作电流恒为I,经监测,入口处的含尘气体的PM值为k1,出口处的洁净气体的PM值降为k2,若视细颗粒物均为直径为D、密度为ρ的均匀球体,且不计相互之间的影响,忽略含尘气体带入的电荷.
空气中直径小于等于 2.5 微米的细颗粒物称做PM2.5,其在空气中的含量称作PM值,单位是毫克每立方米.某校“PM2.5兴趣小组”自制了一台静电除尘器,装置呈圆筒形,如图为其截面图.高压电极的负极位于中轴线上,由A、B两段金属构成,A段较粗呈杆状,B段较细呈针状,收尘区由半径为R的圆柱形的金属筒壁构成,接高压电源的正极.圆筒中气体分子中的电子和带正电的部分由于受到方向相反的强大的静电力而电离.一部分细颗粒物吸附了电子而带负电,所有带负电的细颗粒物都飞向筒壁,最后在重力的作用下落在筒底,空气因此而变得清洁.在一次试验中,含尘气体由底部吹入,气流速度恒为v,高压电源的恒定不变,工作电流恒为I,经监测,入口处的含尘气体的PM值为k1,出口处的洁净气体的PM值降为k2,若视细颗粒物均为直径为D、密度为ρ的均匀球体,且不计相互之间的影响,忽略含尘气体带入的电荷.