题目内容
12. 如图所示,两轮间距l=5m的水平传送带的主动轮半径为0.1m,正以30rad/s的角速度顺时针转动,质量为m=1kg的小滑块以动能Ek滑上传送带左端B,当小滑块到达传送带右端C时,速度变为4m/s,小滑块与传送带间的动摩擦因数为0.2,重力加速度g=10m/s2,求:
如图所示,两轮间距l=5m的水平传送带的主动轮半径为0.1m,正以30rad/s的角速度顺时针转动,质量为m=1kg的小滑块以动能Ek滑上传送带左端B,当小滑块到达传送带右端C时,速度变为4m/s,小滑块与传送带间的动摩擦因数为0.2,重力加速度g=10m/s2,求:(1)小滑块刚滑上传送带时的动能Ek;
(2)若小滑块刚滑上传送带时的动能是$\frac{1}{36}$Ek,求小滑块从B到C所用的时间,以及小滑块与传送带间由于摩擦产生的热量.
分析 根据牛顿第二定律求出A物块在传送带上的加速度,结合运动学公式求出物块一直做匀减速直线运动到达右端的速度,通过与传送带的速度比较,分析物块的运动规律,通过牛顿第二定律和运动学公式进行求解.
解答 解:(1)设传送带的速度为v0,
传送带的速度:v0=ωr=30×0.1=3m/s
小滑块在传送带上一直做匀减速运动,
对滑块,由牛顿第二定律得:μmg=ma
代入数据解得:a=2m/s2,
由匀变速直线运动的速度位移公式得:v22-v12=2al,
代入数据解得,小滑块的初速度:v1=6m/s,
小滑块的初动能:EK=$\frac{1}{2}$mv12=18J;
(2)若小滑块刚滑上传送带时的动能是$\frac{1}{36}$Ek,
即:$\frac{1}{36}$EK=$\frac{1}{2}$mv2,解得,滑块的初速度:v=1m/s,
滑块速度小于传送带速度,滑块在传送带上做匀加速直线运动,
当滑块速度与传送带速度相等需要的时间:t1=$\frac{{v}_{0}-v}{a}$=1s,
滑块的位移:x1=$\frac{{v}_{0}+v}{2}$t1=2m,
滑块匀速运动的时间:t2=$\frac{{x}_{2}}{{v}_{0}}$=$\frac{l-{x}_{1}}{{v}_{0}}$=1s,
滑块的运动时间:t=t1+t2=1+1=2s,
时间内传送带的位移:x′=v0t1=3×1=3m,
滑块与传送带的相对位移:s=x′-x1=3-2=1m,
系统产生的热量:Q=μmgs=2J;
答:(1)小滑块刚滑上传送带时的动能Ek为18J;
(2)若小滑块刚滑上传送带时的动能是$\frac{1}{36}$Ek,
小滑块从B到C所用的时间为2s,小滑块与传送带间由于摩擦产生的热量为2J.
点评 解决本题的关键通过物体的受力判断出物体滑上传送带的运动情况,结合牛顿第二定律和运动学公式进行求解.

 如图所示,一辆汽车 以10m/s的速度沿平直公路行驶,遇障碍刹车后获得大小为4m/s2的加速度.刹车后3s内,汽车走过的路程为( )
如图所示,一辆汽车 以10m/s的速度沿平直公路行驶,遇障碍刹车后获得大小为4m/s2的加速度.刹车后3s内,汽车走过的路程为( )| A. | 12m | B. | 12.5m | C. | 90m | D. | 126m |
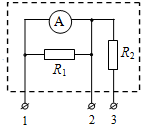 如图所示,其中电流表A的量程为0.6A,表盘均匀划分为30个小格,每一小格表示0.02A;R1的阻值等于电流表内阻的$\frac{1}{2}$;R2的阻值等于电流表内阻的2倍.若用电流表A的表盘刻度表示流过接线住1的电流值,则下列分析正确的是( )
如图所示,其中电流表A的量程为0.6A,表盘均匀划分为30个小格,每一小格表示0.02A;R1的阻值等于电流表内阻的$\frac{1}{2}$;R2的阻值等于电流表内阻的2倍.若用电流表A的表盘刻度表示流过接线住1的电流值,则下列分析正确的是( )| A. | 将接线住1、2接入电路时,每一小格表示0.04A | |
| B. | 将接线住1、2接入电路时,每一小格表示0.02A | |
| C. | 将接线住1、3接入电路时,每一小格表示0.06A | |
| D. | 将接线住1、3接入电路时,每一小格表示0.01A |
| A. | 当分子间距离r<r0时分子间只有分子斥力作用 | |
| B. | 分子间距离增大时分子势能增大 | |
| C. | 温度越高分子的平均动能越大 | |
| D. | 温度高的物体的内能一定比温度低的物体内能大 |
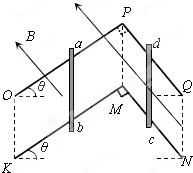 如图所示,平行金属导轨OP、KM和PQ、MN相互垂直,且OP、KM与水平面间夹角为θ=37°,导轨间距均为L=1m,电阻不计,导轨足够长.两根金属棒ab和cd与导轨垂直放置且接触良好,ab的质量为M=2kg,电阻为R1=2Ω,cd的质量为m=0.2kg,电阻为R2=1Ω,金属棒和导轨之间的动摩擦因数均为μ=0.5,两个导轨平面均处在垂直于轨道平面OPKM向上的匀强磁场中.现让cd固定不动,将金属棒ab由静止释放,当ab沿导轨下滑x=6m时,速度已达到稳定,此时,整个回路消耗的电功率为P=12W.求:
如图所示,平行金属导轨OP、KM和PQ、MN相互垂直,且OP、KM与水平面间夹角为θ=37°,导轨间距均为L=1m,电阻不计,导轨足够长.两根金属棒ab和cd与导轨垂直放置且接触良好,ab的质量为M=2kg,电阻为R1=2Ω,cd的质量为m=0.2kg,电阻为R2=1Ω,金属棒和导轨之间的动摩擦因数均为μ=0.5,两个导轨平面均处在垂直于轨道平面OPKM向上的匀强磁场中.现让cd固定不动,将金属棒ab由静止释放,当ab沿导轨下滑x=6m时,速度已达到稳定,此时,整个回路消耗的电功率为P=12W.求: 如图所示,一质量为2kg的物体静止在水平地面,在14N的水平力作用下开始运动,运动过程中受到的阻力为8N.
如图所示,一质量为2kg的物体静止在水平地面,在14N的水平力作用下开始运动,运动过程中受到的阻力为8N.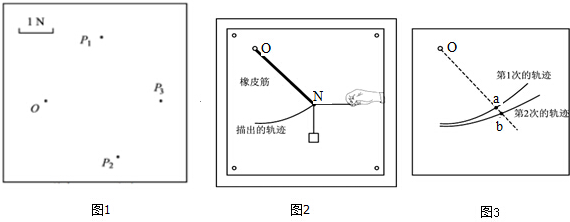
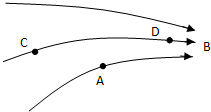 如下图所示的磁感线中,请画出A点的磁感应强度的方向,比较C点和D点的磁感应强度的大小:BC< BD(填“>”“<”或“=”).
如下图所示的磁感线中,请画出A点的磁感应强度的方向,比较C点和D点的磁感应强度的大小:BC< BD(填“>”“<”或“=”). 一辆汽车以54km/h的速率通过一座拱桥的桥顶,汽车对桥面的压力等于车重的一半,这座拱桥的半径是多少?若要使汽车过桥顶时对桥面无压力,则汽车过桥顶时的速度大小至少是多少?
一辆汽车以54km/h的速率通过一座拱桥的桥顶,汽车对桥面的压力等于车重的一半,这座拱桥的半径是多少?若要使汽车过桥顶时对桥面无压力,则汽车过桥顶时的速度大小至少是多少?