题目内容
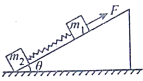
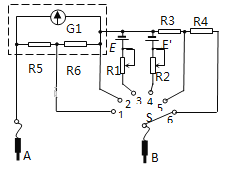
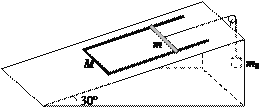
【题目】如下图所示,质量为M的“U”形金属导轨放置在倾角为30°的光滑斜面上,导轨间距为d,导轨间存在垂直斜面的磁感应强度为B的匀强磁场,导轨上垂直于导轨平放质量为m的导体棒,跨过滑轮的细绳一端悬挂质量为m0的物块,另一端通过平行于斜面的细绳连接导体棒,已知m0=3m,M=4m,重力加速度为g,导体棒电阻为R,其余电阻不计,导轨与导体棒之间的摩擦力不计,运动过程中导体棒未滑出导轨,导轨与物块均未落地。
(1)若导轨固定,由静止释放导体棒,求导体棒运动的最大速度的大小;
(2)若将导轨和导体棒同时由静止释放,导轨沿斜面向下运动达到最大速度v1时,求导体棒的速度v2和加速度a2。
(3)在导体棒运动过程中选择不同时刻释放导轨,导轨可能由静止沿斜面向下运动,也可能由静止沿斜面向上运动。要保证任何时刻释放导轨都能由静止沿斜面向下运动,求斜面倾角的取值范围。
【答案】(1)![]() (2)
(2)![]() -v1
-v1 ![]() (3)θ>37°
(3)θ>37°
【解析】(1)释放导体棒后,导体棒做加速度减小的加速运动,加速度为零时,速度最大,设为![]()
则根据法拉第电磁感应定律可以得到: ![]()
根据闭合电路欧姆定律: ![]()
安培力公式: ![]()
则速度最大时: ![]()
解得![]()
(2)导轨向下速度最大时,则根据法拉第电磁感应定律可以得到![]()
根据闭合电路欧姆定律: ![]()
则: ![]()
对物块根据牛顿第二定律:m0g-T=m0a2
对导体棒根据牛顿第二定律:T-F安-mgsinθ=ma2
对导轨F安=Mgsinθ
解得: ![]() ,
, ![]() ,
,
(3)导体棒运动过程中,导轨受到沿斜面向上的安培力。若导体棒速度最大时,释放导轨能向下运动,则满足要求。
此时m0g=F+mgsinθ,
只需F <Mgsinθ
解得![]() 即
即![]()

练习册系列答案
相关题目