题目内容
13.滴水法测重力加速度的过程是这样的,让水龙头的水一滴一滴的滴在其正下方的盘子里,调整水龙头到盘子的距离,让前一滴水滴到盘子里而听到声音时,后一滴恰好离开水龙头.测出从第一次听到声音到第n次听到水击盘声的总时间为t,用刻度尺量出水龙头口到盘子的高度差h,即可算出重力加速度.则重力加速度的计算公式是g=$\frac{2h{(n-1)}^{2}}{{t}^{2}}$;如果使一滴水碰到盘子时恰好有另一滴水刚好从水龙头滴下,而空中还有一个正在下落中的雨滴,同样用刻度尺量出水龙头口到盘子的高度差h,再用秒表测时间,以第一个水滴离开水龙头开始计时,到第n个水滴落在盘中,共用时间为t,则重力加速度的计算公式为g=$\frac{h{(N+1)}^{2}}{2{t}^{2}}$.
分析 前一滴水滴到盘子里面听到声音时后一滴水恰好离开水龙头,测出n次听到水击盘的总时间为t,知道两滴水间的时间间隔,根据h=$\frac{1}{2}{gt}^{2}$求出重力加速度.
当一滴水碰到盘子时,恰好有另一滴水从水龙头开始下落,而空中还有一滴正在下落的水滴,从第一滴水离开水龙头开始,到第N滴水落至盘中(即N+2滴水离开水龙头),共用时间为t(s),知道两滴水间的时间间隔,根据h=$\frac{1}{2}$gt2求出重力加速度.
解答 解:从前一滴水滴到盘子里面听到声音时后一滴水恰好离开水龙头,测出n次听到水击盘的总时间为t,知道两滴水间的时间间隔为△t=$\frac{t}{n-1}$,所以水从水龙头到盘子的时间为t=$\frac{t}{n-1}$,
h=$\frac{1}{2}{gt}^{2}$得:g=$\frac{2h{(n-1)}^{2}}{{t}^{2}}$;
从第一滴水离开水龙头开始,到第N滴水落至盘中(即N+2滴水离开水龙头),共用时间为t(s),知道两滴水间的时间间隔为△t=$\frac{t}{N+1}$,所以水从水龙头到盘子的时间为t′=$\frac{2t}{N+1}$,根据h=$\frac{1}{2}$gt′2,g=$\frac{2h}{t{′}^{2}}$=$\frac{2h}{\frac{4{t}^{2.}}{{(N+1)}^{2}}}$=$\frac{2h(N+1)^{2}}{4{t}^{2}}$=$\frac{h{(N+1)}^{2}}{2{t}^{2}}$.
故本题答案为:$\frac{2h{(n-1)}^{2}}{{t}^{2}}$;$\frac{h{(N+1)}^{2}}{2{t}^{2}}$.
点评 解决本题的关键明确实验原理,找出对应的实验方法,再由相应的自由落体规律进行分析求解即可.

 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
| A. | A 球刚滑至水平面时的速度大小为$\frac{{\sqrt{5gR}}}{2}$ | |
| B. | B 球刚滑至水平面时的速度大小为$\frac{{\sqrt{6gR}}}{2}$ | |
| C. | 在A 球沿斜面下滑的过程中,轻绳对B 球先做正功、后不做功 | |
| D. | 两小球在水平面上不可能相撞 |

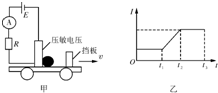 压敏电阻的阻值随所受压力的增大而减小,有位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图甲所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图乙所示,则t1~t2时间内小车的运动情况是变加速(选填“匀速”、“匀加速”或“变加速”);t2~t3时间内小车的运动情况是匀加速(选填“匀速”、“匀加速”或“变加速”)
压敏电阻的阻值随所受压力的增大而减小,有位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图甲所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图乙所示,则t1~t2时间内小车的运动情况是变加速(选填“匀速”、“匀加速”或“变加速”);t2~t3时间内小车的运动情况是匀加速(选填“匀速”、“匀加速”或“变加速”)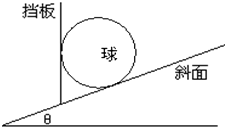 将一光滑小球放在挡板和斜面之间,如图所示,已知小球重力为G,斜面倾角为θ.尝试求解下列问题:
将一光滑小球放在挡板和斜面之间,如图所示,已知小球重力为G,斜面倾角为θ.尝试求解下列问题: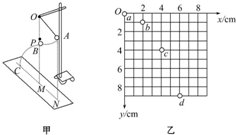 某同学在一个未知星球上用如图甲所示装置研究平抛运动的规律.悬点O正下方P点处有水平放置的炽热电热丝,当悬线摆至电热丝处时能轻易被烧断,小球由于惯性向前飞出做平抛运动.现对小球采用频闪数码照相机连续拍摄.在有坐标纸的背景屏前,拍下了小球在做平抛运动过程中的多张照片,经合成后,照片如图乙所示.a、b、c、d为连续四次拍下的小球位置,已知照相机连续拍照的时间间隔是0.10s,照片大小如图中坐标所示,又知该照片的长度与实际背景屏的长度之比为1:4,则:
某同学在一个未知星球上用如图甲所示装置研究平抛运动的规律.悬点O正下方P点处有水平放置的炽热电热丝,当悬线摆至电热丝处时能轻易被烧断,小球由于惯性向前飞出做平抛运动.现对小球采用频闪数码照相机连续拍摄.在有坐标纸的背景屏前,拍下了小球在做平抛运动过程中的多张照片,经合成后,照片如图乙所示.a、b、c、d为连续四次拍下的小球位置,已知照相机连续拍照的时间间隔是0.10s,照片大小如图中坐标所示,又知该照片的长度与实际背景屏的长度之比为1:4,则: 如图所示的电路中,电源的电动势E=1.5V,内电阻r=5Ω,外电路的电阻R1=15Ω,R2=30Ω.求电路中的总电流和路端电压.
如图所示的电路中,电源的电动势E=1.5V,内电阻r=5Ω,外电路的电阻R1=15Ω,R2=30Ω.求电路中的总电流和路端电压.