题目内容
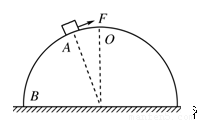
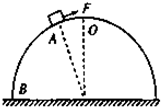 如图所示,上表面粗糙的半圆柱体放在水平面上,小物块从半圆柱体上的A点,在外力F作用下沿圆弧向下滑到B点,此过程中F始终沿圆弧的切线方向且半圆柱体保持静止状态,小物块运动的速率不变,则( )
如图所示,上表面粗糙的半圆柱体放在水平面上,小物块从半圆柱体上的A点,在外力F作用下沿圆弧向下滑到B点,此过程中F始终沿圆弧的切线方向且半圆柱体保持静止状态,小物块运动的速率不变,则( )| A、半圆柱体对小物块的支持力逐渐变大 | B、半圆柱体对小物块的摩擦力变大 | C、外力F变大 | D、小物块所受的合外力变小 |
分析:先对小滑块受力分析,滑块做匀速率圆周运动,根据径向合力提供向心力和切向合力为零,列式支持力和拉力的表达式,再进行分析.
解答: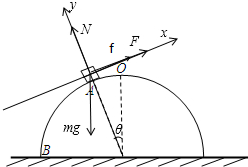 解:A、B、C、对小物块受力分析,受到重力、支持力、摩擦力和拉力,如图物块做匀速圆周运动,径向合力提供向心力,切向合力为零,则根据牛顿第二定律有:
解:A、B、C、对小物块受力分析,受到重力、支持力、摩擦力和拉力,如图物块做匀速圆周运动,径向合力提供向心力,切向合力为零,则根据牛顿第二定律有:
mgcosθ-N=m
①
F+f-mgsinθ=0 ②
由①得,N=mgcosθ-m
,由于θ越来越大,故支持力N变小;
由f=μN,知f变小.
由②得:F=mgsinθ-f=mgsinθ-f,θ增大,sinθ增大,f变小,则拉力F变大,故AB错误,C正确;
D、物块做匀速圆周运动,合外力提供向心力,由F外=m
知,合外力大小不变.故D错误.
故选:C.
 解:A、B、C、对小物块受力分析,受到重力、支持力、摩擦力和拉力,如图物块做匀速圆周运动,径向合力提供向心力,切向合力为零,则根据牛顿第二定律有:
解:A、B、C、对小物块受力分析,受到重力、支持力、摩擦力和拉力,如图物块做匀速圆周运动,径向合力提供向心力,切向合力为零,则根据牛顿第二定律有:mgcosθ-N=m
| v2 |
| R |
F+f-mgsinθ=0 ②
由①得,N=mgcosθ-m
| v2 |
| R |
由f=μN,知f变小.
由②得:F=mgsinθ-f=mgsinθ-f,θ增大,sinθ增大,f变小,则拉力F变大,故AB错误,C正确;
D、物块做匀速圆周运动,合外力提供向心力,由F外=m
| v2 |
| R |
故选:C.
点评:本题关键是对小物块受力分析,然后根据牛顿第二定律和向心力公式列式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
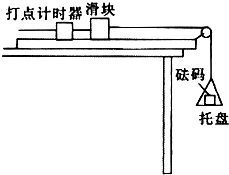 某物理研究性学习小组在探究活动中测量滑块与木块之间的动摩擦因数,实验装置如图所示,一表面粗糙的木板固定在水平桌面上,一端装有定滑轮;木板上有一滑块,其一端与电磁打点计时器的纸带相连,另一端通过跨过定滑轮的细线与托盘连接,打点计时器使用的交流电源的频率为50Hz,实验时,在托盘中放入适量砝码,滑块做匀加速直线运动,在纸带上打出一系列小点.
某物理研究性学习小组在探究活动中测量滑块与木块之间的动摩擦因数,实验装置如图所示,一表面粗糙的木板固定在水平桌面上,一端装有定滑轮;木板上有一滑块,其一端与电磁打点计时器的纸带相连,另一端通过跨过定滑轮的细线与托盘连接,打点计时器使用的交流电源的频率为50Hz,实验时,在托盘中放入适量砝码,滑块做匀加速直线运动,在纸带上打出一系列小点.