题目内容
【题目】如图所示,两根长度分别为2l和l的轻杆一端固定在一起,构成夹角为60°的支架,该支架可绕固定轴O在竖直平面内无摩擦转动,两根轻杆的另一端分别固定着质量为m的小球甲和质量为2m的小球乙。将连接小球甲的轻杆转动到水平位置,然后由静止释放,已知重力加速度为g,不计空气阻力,则下列说法正确的是( )
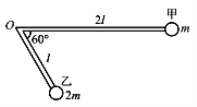
A.当整个系统第一次速度为0时,小球乙的位置与固定轴O位于同一高度处
B.当整个系统第一次速度为0时,小球乙的位置比固定轴O的位置高
C.当小球乙摆到最低点时,轻杆对小球乙的弹力不沿杆方向
D.从静止开始至小球甲速度最大时,支架对小球甲所做的功为![]()
【答案】ACD
【解析】
AB.设小球乙与O点等高时速度为v,则小球甲的速度为2v,系统从静止开始至小球乙与O点等高的过程,如图a所示
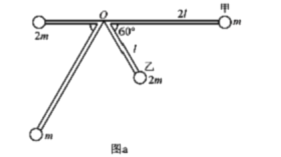
由机械能守恒定律得
![]()
解得
![]()
故A项正确,B项错误;
C.如图b所示
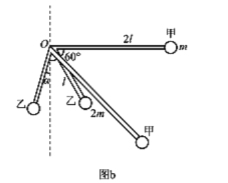
设小球乙与竖直方向成α角时,小球甲和小球乙的速度最大,对系统由机械能守恒定律得
![]()
整理后得
![]()
其中
![]()
所以
![]()
当
![]()
时,速度最大
![]()
所以当小球乙第一次摆至最低点时,速度还在增大,所以沿轨迹切向方向上的合力不为零,而重力沿竖直方向,所以轻杆对小球乙的弹力不沿杆方向,C项正确;
D.对小球甲从静止至速度最大的过程,由动能定理得
![]()
解得
![]()
所以D项正确。
故选ACD。

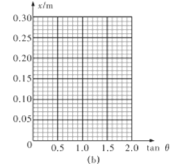
【题目】如图(a)所示,AB是一可升降的竖直支架,支架顶端A处固定一弧形轨道,轨道末端水平。一条形木板的上端铰接于过A的水平转轴上,下端搁在水平地面上。将一小球从弧形轨道某一位置由静止释放,小球落在木板上的某处,测出小球平抛运动的水平射程x和此时木板与水平面的夹角θ,并算出 tanθ。改变支架AB的高度,将小球从同一位置释放,重复实验,得到多组x和tanθ,记录的数据如下表:
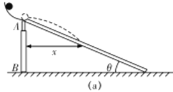
实验次数 | 1 | 2 | 3 | 4 | 5 | 6 |
tanθ | 0.18 | 0.32 | 0.69 | 1.00 | 1.19 | 1.43 |
x/m | 0.035 | 0.065 | 0.140 | 0.160 | 0.240 | 0.290 |
(1)在图(b)的坐标中描点连线,作出x— tanθ的关系图象。
(____)
(2)根据x—tanθ图象可知小球做平抛运动的初速度v0= ___m/s;实验中发现θ超过60°后,小球将不会掉落在斜面上,则斜面的长度为____m。(重力加速度g取10 m/s2)
(3)实验中有一组数据出现明显错误,可能的原因是______。