题目内容
【题目】如图是某游乐场的一种过山车的简化图,过山车由倾角为θ的斜面和半径为R的光滑圆环组成0.假设小球从A处由静止释放,沿着动摩擦因数为μ的斜面运动到B点(B为斜面与圆环的切点),而后沿光滑圆环内侧运动,若小球刚好能通过圆环的最高点C,求:(重力加速度为g)
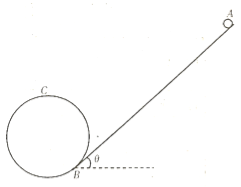
(1)小球沿斜面下滑的加速度的大小;
(2)斜面的长度至少为多大.
【答案】(1)小球沿斜面下滑的加速度的大小是g(sinθ﹣μcosθ);
(2)斜面的长度至少为![]() .
.
【解析】
试题分析:(1)根据牛顿第二定律求解小球沿斜面下滑的加速度的大小.
(2)小球刚好能通过圆环的最高点C,由重力提供向心力,由牛顿第二定律可求出小球经过C点时的速度,对全过程运用动能定理可求出斜面的长度.
解;(1)由牛顿第二定律得
mgsinθ﹣μmgcosθ=ma
解得 a=g(sinθ﹣μcosθ)
(2)设斜面的最小长度为L.小球在最高点C时,由牛顿第二定律得
mg=m![]()
对全过程,根据动能定理得
mg[Lsinθ﹣R(1+cosθ)]﹣μmgcosθ=![]()
联立上两式得,L=![]()
答:
(1)小球沿斜面下滑的加速度的大小是g(sinθ﹣μcosθ);
(2)斜面的长度至少为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目