题目内容
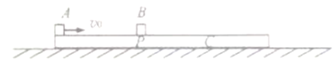
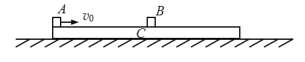
【题目】一足够长木板C静止在光滑水平面上,如图所示,距C的左端![]() 处的P点放有一物块B,物块A以水平初速度v0=3m/s滑上木板的最左端,A、B、C质量相等,物块A、B与木板C间的动摩擦因数均为μ=0.2,A、B均可看做质点,重力加速度为g=10m/s2。求:
处的P点放有一物块B,物块A以水平初速度v0=3m/s滑上木板的最左端,A、B、C质量相等,物块A、B与木板C间的动摩擦因数均为μ=0.2,A、B均可看做质点,重力加速度为g=10m/s2。求:
(1)物块A滑上C后一小段时间内,A、B、C的加速度大小;
(2)通过计算判断A,B是否会相碰;
(3)若不能相碰,求出最终A、B间的距离;若能相碰,A、B将粘在一起运动,求出最终AB距P点的距离。
【答案】(1)![]() ,
,![]() ;(2)A、B一定相碰;(3)
;(2)A、B一定相碰;(3)![]()
【解析】
(1)A滑上C后水平方向受向左的滑动摩擦力
![]()
解得
![]()
若B、C相对静止,则B、C整体受A对它的向右的滑动摩擦力,即:
![]()
解得
![]()
由题意可知B与C间的动摩擦因数也为0.2,故B在C表面的最大加速度为
![]()
故![]() 可以保持相对静止,即
可以保持相对静止,即
![]()
(2)假设A与B、C速度相等时刚好与B相碰,设此时速度为![]() ,A在C上滑行了距离x,则由A、B、C动量守恒可知
,A在C上滑行了距离x,则由A、B、C动量守恒可知
![]()
解得
![]()
由系统能量守恒可知
![]()
解得
![]()
故A、B一定相碰.
(3)设A、B相碰前的速度分别为![]() 、
、![]() (此时B、C相对静止,故速度相等),由系统动量守恒和能量守恒得
(此时B、C相对静止,故速度相等),由系统动量守恒和能量守恒得
![]()
![]()
解得
![]()
![]()
设![]() 相碰后粘在一起的速度为
相碰后粘在一起的速度为![]() ,由动量守恒得
,由动量守恒得
![]()
解得
![]()
由(2)中讨论可知,最终![]() 相对静止时的共同速度为
相对静止时的共同速度为![]() ,由(3)中讨论可知A、B相碰时C的速度为
,由(3)中讨论可知A、B相碰时C的速度为![]() ,设
,设![]() 与C相对静止时距P点的距离为x,由动能定理得
与C相对静止时距P点的距离为x,由动能定理得
![]()
解得
![]() .
.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目