题目内容
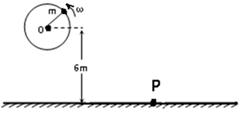
一个人用一根长L=1m，只能承受T=46N拉力的绳子，拴着一个质量为m=1kg的小球，在竖直面内做圆周运动，已知转轴O离地的距离H=6m，如图所示，此人必须用多大的角速度转动小球方能使小球到达最低点时绳子被拉断，绳子拉断后，小球的水平射程是多大？
【答案】
所以，小球的水平射程为 s = v t
= 6 m
6 m
【解析】
试题分析：设小球经过最低点的角速度为ω，速度为v时，绳子刚好被拉断，则
由牛顿第二定律 F = m a得
T – m g = mω2L
∴ 
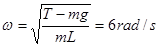v
= ωL = 6 m/s
小球脱离绳子的束缚后，将做平抛运动，其飞行时间为
|
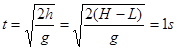
考点：考查对圆周运动规律的应用
点评：本题难度较小，明确绳子刚好断裂时小球所受合力的大小和方向，根据合力提供向心力求得此时的线速度，小球飞出后做的是平抛运动，再根据平抛运动规律求解，对于这种多过程问题要分段求解
练习册系列答案
相关题目
如图所示，一个人用一根长L=lm，最大只能承受T=74N拉力的绳子，拴着一个质量m=1kg的小球，在竖直平面内做圆周运动．已知圆心O离地面的高度h=6m，g=10m/s2．求：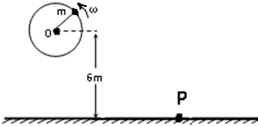
如图所示，一个人用一根长L=1m，只能承受T=46N拉力的绳子，拴着一个质量为m=1kg的小球，在竖直面内做逆时针方向的圆周运动，已知圆心O离地的距离H=6m，g=10m/s2．
