��Ŀ����
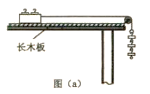
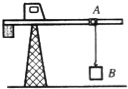
����Ŀ����ͼ������������һ������ˮƽ�����˶���С��A��С����װ�е�������B�ĵ�������С��A������B����ͬ��ˮƽ�ٶ��ص��۷��������˶���ͬʱ������������B���ϵ���A��B֮��ľ�����d=H��2t2��SI����SI��ʾ���ʵ�λ�ƣ�ʽ��HΪ���������ĸ߶ȣ����ɱ仯������������ ��
A���ٶȴ�С�����ֱ���˶�
B���ٶȴ�С���ӵ������˶�
C�����ٶȴ�С���������������˶�
D�����ٶȴ�С��������仯�������˶�
���𰸡�BC
��������
���������A��B������B�μ����������˶���ˮƽ���������ֱ���˶�����ֱ������ȼ���ֱ���˶���
������ֱ���˶������λ�Ʃ�ʱ���ϵ��ʽx=v0t+![]() at2���ɵõ�
at2���ɵõ�
d=H��x=H����v0yt+![]() at2�� ��
at2�� ��
�ָ�������
d=H��2t2 ��
���ԵöԱȢ٢���ʽ�ɵó���
��ֱ���˶��ļ��ٶȵĴ�СΪ
ay=4m/s2
��ֱ���˶��ij��ٶ�Ϊ
v0y=0
����ֱ���ٶ�Ϊ
vy=4t
�����ˮƽ���ٶȲ���
���˶����ٶ�Ϊ��ֱ���ٶ���ˮƽ���ٶȵĺ��ٶȣ���ѭƽ���ı��ζ��ʺ��ٶȵķ��ϱ仯������һ���������˶������ٶȵĴ�Сv=![]() ���ʺ��ٶȵĴ�СҲһ�����ϱ��A����B��ȷ��
���ʺ��ٶȵĴ�СҲһ�����ϱ��A����B��ȷ��
C��D��ˮƽ�ּ��ٶȵ����㣬�ʺϼ��ٶȵ�����ֱ���˶��ļ��ٶȣ�����ϼ��ٶȵĴ�С�ͷ����䣬��C��ȷ��D����
��ѡ��BC��

����Ŀ��ijͬѧ������ͼ��ʾ��װ��̽�������ٶȱ仯�Ĺ�ϵ��

������С�������Ƥ��������µ�������ˮƽ���滬�У�֮��ƽ������ˮƽ�����ϣ�����ΪM1��
�������ڶ����Ϸֱ�����2����3����4������ͬ������Ƥ�ʹÿ����Ƥ������ij��ȶ�����һ�£��ظ����裨������С������ֱ��ΪM2��M3��M4������
����������������ݣ��������ݴ�����
��1��Ϊ���С����׳�ʱ�Ķ��ܣ�����Ҫ���������������е� ������ȷ�𰸱�ţ���
A����������m |
B����Ƥ���ԭ��x |
C����Ƥ����쳤����x |
D�����浽����ĸ߶�h |
E��С����׳��㵽��ص��ˮƽ����L
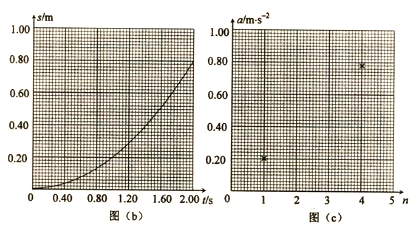
��2��������ʵ������Ƥ���С��������ֱ��ΪW1��W2��W3��������С����׳��㵽��ص��ˮƽ����ֱ��ΪL1��L2��L3���������������ٶȵ�ƽ�������ȣ���Ӧ��WΪ�����ꡢ Ϊ��������ͼ�����ܵõ�һ��ֱ�ߡ�
��3������С���������֮���Ħ�����ܺ��ԣ����ɴ������������� ������żȻ���������ϵͳ���������