��Ŀ����
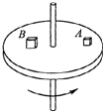
����Ŀ����ͼ��ʾ��x����ˮƽ���ʹ��غϣ�����ԭ��O�ڴ��ʹ�����ˣ����ʹ���L=8m�����Ժ㶨������ת��һ����m=1kg��С���������ڴ��ʹ��Ϻ�����ΪxP=2m��P�㣬С����洫�ʹ��˶���Q���ǡ���ܳ��ϰ뾶ΪR=0.5m�Ĺ⻬Բ���������ߵ�N�㣮С����봫�ʹ���Ķ�Ħ��������=0.5���������ٶ�g=10m/s2 �� ��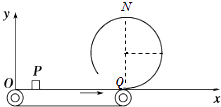
��1�����ջ���Բ�����ʱ���ٶȴ�С��
��2�����ʹ���ת�����ʣ�
��3������С�������ڴ��ʹ��ϵ���һλ�ã�С���ǡ�ܵ���Բ���������Բ�ĵȸߵ�M�㣨��ͼ��������������λ�õĺ������Ƕ��٣�����������ջ���Բ�����ʱ��Բ�������͵��ѹ�����
���𰸡�
��1��
�⣺С���ǡ�ó���Բ���������ߵ㣬�����ṩ��������
��ţ�ٵڶ����ɵã�mg=m ![]() ��
��
����Q��N������У���е���غ㣬
�ɻ�е���غ㶨�ɵã� ![]() mvQ2=mg2R+
mvQ2=mg2R+ ![]() mvN2��
mvN2��
�������ݽ�ã�vQ=5m/s
��2��
�⣺С����ڴ��ʹ����������˶���
��ţ�ٵڶ����ɵã���mg=ma����ã�a=5m/s2��
����ٶȴﵽ5m/s����ʱ�䣺t= ![]() =
= ![]() =1s��
=1s��
�ù���λ�ƣ�x= ![]() at2=
at2= ![]() ��5��12=2.5m��L��xP=6m��
��5��12=2.5m��L��xP=6m��
���ʹ��ٶ�v0=vQ=5m/s
��3��
�⣺����鿪ʼ�˶�������M������У�
�ɶ��ܶ����ã���mg��L��x�䣩��mgR=0��0����ã�x��=7m��
����鿪ʼ�˶�������Բ����͵�����У��ɶ��ܶ����ã�
��mg��L��x�䣩= ![]() mv2��0��
mv2��0��
��Բ����͵㣬��ţ�ٵڶ����ɵã�
F��mg=m ![]() ����ã�F=30N��
����ã�F=30N��
��ţ�ٵ������ɿ�֪�����Թ����ѹ��F��=F=30N��������ֱ���£�
����������1����ţ�ٵڶ����������鵽��N����ٶȣ��ɻ�е���غ㶨�������Q����ٶȣ���2����ţ�ٵڶ�����������ٶȣ������ȱ����˶���λ�ƹ�ʽ���λ�ƣ�Ȼ��������⣮��3���ɶ��ܶ������λ�ƣ���ţ�ٵڶ��������֧������Ȼ����ţ�ٵ����������ѹ����
�����㾫����ͨ��������ö��ܶ������ۺ�Ӧ�úͻ�е���ۺ�Ӧ�ã�����Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�ϵͳ��̬���ܻ�е��E 1 ����ĩ̬���ܻ�е��E 2 ����E1 =E2��ϵͳ���ٵ����������ܦ�E P�� ����ϵͳ���ӵ��ܶ��ܦ�E K�� ������E P�� =��E K������ϵͳֻ��A��

����Ŀ������ѡ����ʷʵ�����֮������ϵ��ȷ����
ʷʵ | ���� | |
A | ����ᡰ����˵������� | Ϊ�����ṩ�˱�֤���������;�� |
B | ţ�پ�����ѧ��ϵ�Ľ��� | ��־�������ѧʱ���Ŀ�ʼ |
C | �����ڷ��ֵ�Ÿ�Ӧ���� | Ϊ��ҵ�����Ŀ�չ�춨�����ۻ��� |
D | ����˹̹����۵Ĵ��� | �ı����˶��������������λ�õĿ��� |
A.AB.BC.CD.D